Qual o menor número de pesagens para descobrir a moeda mais leve?
Estava eu no scroll hell do Instagram quando me deparei com este reels propondo um desafio (que sumarizei neste post no BlueSky):
Eu te dou 8 moedas, só que tem um catch! Uma delas tem um peso menor que as outras. Também dou uma balança de pratos tal qual abaixo. Descubra a de menor peso em no máximo 2 pesagens.
E… que tal descobrir a menor moeda em 5 pesadas ou menos para 100 moedas? Ou 7 ou menos para 1000 moedas?
Ou então, se existir uma moeda diferente, seja para mais ou menos (mas que você não sabe a priori para qual lado), como fazer de modo ótimo?
Vamos primeiro explorar para o mundo da moeda mais leve, vamos chegar em um algoritmo interessante, e então vamos depois analisar a questão de não saber se a moeda diferente é por mais ou por menos peso.
Solução mais básica
A solução mais básica para o problema: pegar uma moeda e pesar com todas as outras.
Tendo 8 moedas, vamos separar 1 para servir de base. Se a balança der igual, então já sabemos que que as duas moedas tem o mesmo peso, então posso separar/descartar a moeda que eu puxei.
Isso significa que vão ser necessárias até 7 pesagens!
Algoritmicando
Basicamente, vamos precisar de um repositório de moedas para serem removidas,
um repositório de moedas para serem depositadas de modo intermediário, a
balança e vamos retornar o identificador da moeda. O que vai identificar a
moeda? Tanto faz, podemos supor que ela tenha um campo chamado moeda.id. Pode
ser o índice da moeda dentro da coleção em que ela se situa, isso vai ser
transparente para a questão.
Então, vamos lá. De fora vem a balança e o saco de moedas. O saco eu posso fazer as seguintes operações:
- perguntar se tá vazio
- pegar uma moeda
A balança vai ser uma função da seguinte forma:
type Balanca = (esquerda: Moeda[], direita: Moeda[]) => Pesada;
type Pesada = "DESCEU_ESQUERDA" | "DESCEU_DIREITA" | "EQUILIBRIO";
Então, esse esquema de pesagem seria algo mais ou menos assim:
function achaMoedaMenor(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void): void {
const moedaBase = sacolaDeMoedas.pegaMoeda(); // pega uma moeda da sacola
// essa vai ser a moeda que
// vou usar de base para as medidas
while (!sacolaDeMoedas.vazio()) {
const moedaComparacao = sacolaDeMoedas.pegaMoeda(); // vou comparar com essa
const resultadoComparacao = scale([moedaBase], [moedaComparacao]);
if (resultadoComparacao == "EQUILIBRIO") {
continue;
} else if (resultadoComparacao == "DESCEU_ESQUERDA") {
// desceu para a esquerda
// portanto [moedaBase] mais pesado do que [moedaComparacao]
callback(moedaComparacao);
break;
} else {
// desceu para a direita (por esgotamento)
// portanto [moedaComparacao] mais pesado do que [moedaBase]
callback(moedaBase);
break;
}
}
}
Esse algoritmo itera por no máximo a quantidade de moedas na sacola.
Mas, se eu já descobri que a moeda tem o mesmo peso que a outra, posso descartar as duas! Já que só tem uma com peso diferente.
Melhorando por 2
Bem, vamos descartar ambos nesse caso de pesos iguais.
Basicamente, vamos ter uma espécie de máquina de estado:
- primeiro retiramos uma moeda
- se não estiver vazio, removemos outra moeda
- pesamos
- se o peso for idêntico, volta pro primeiro estado
Um esquema de desenho seria esse:
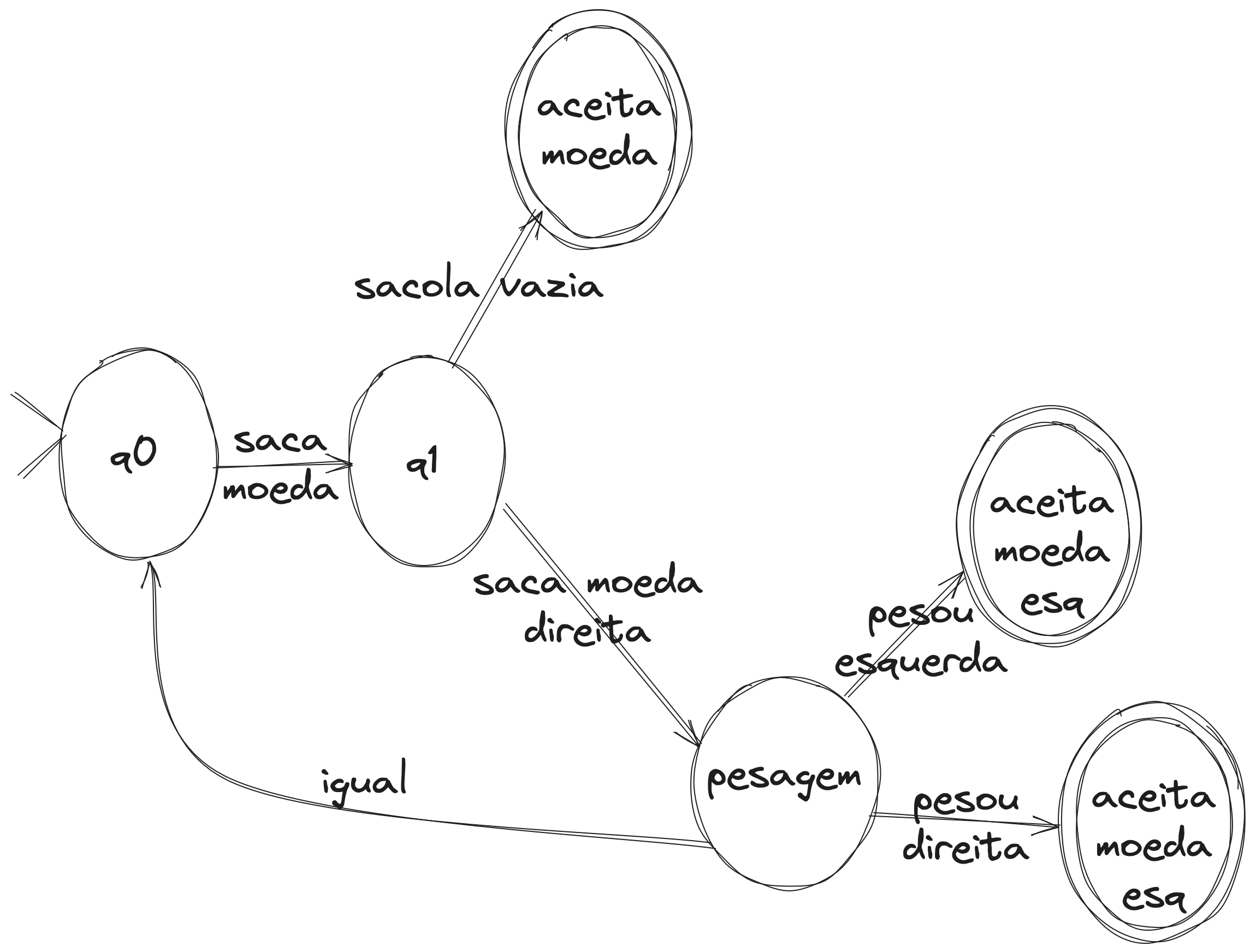
Então, como poderíamos codificar isso? Vamos fazer chamadas de cauda próprias (sabe o que é? olha aqui Otimização de função de cauda em uma toy function) por uma questão de organização do algoritmo:
function achaMoedaMenor(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void): void {
// nesse esquema, isso aqui seria o estado q0
const moedaEsquerda = sacolaDeMoedas.pegaMoeda();
saqueiMoedaEsquerda(sacolaDeMoedas, scale, callback, moedaEsquerda);
}
function saqueiMoedaEsquerda(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void, moedaEsquerda: Moeda): void {
// nesse esquema, isso aqui seria o estado q1
// verificando qual o próximo estado
if (sacolaDeMoedas.vazio()) {
// vazio, portanto aqui seria o estado "aceita moeda"
callback(moedaEsquerda);
} else {
const moedaDireita = sacolaDeMoedas.pegaMoeda();
preparaPesagem(sacolaDeMoedas, scale, callback, moedaEsquerda, moedaDireita);
}
}
function preparaPesagem(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void, moedaEsquerda: Moeda, moedaDireita: Moeda): void {
// nesse esquema, isso aqui seria o estado pesagem
const resultadoComparacao = scale([moedaEsquerda], [moedaDireita]);
if (resultadoComparacao == "EQUILIBRIO") {
// deu igual, vamos descartar as duas moedas e começar de novo
achaMoedaMenor(sacolaDeMoedas, scale, callback);
} else if (resultadoComparacao == "DESCEU_ESQUERDA") {
// desceu para a esquerda
// portanto [moedaEsquerda] mais pesado do que [moedaDireita]
callback(moedaComparacao);
} else {
// desceu para a direita (por esgotamento)
// portanto [moedaDireita] mais pesado do que [moedaEsquerda]
callback(moedaDireita);
}
}
Aqui fazemos a metade das comparações. Mas ainda assim, para achar a menor moeda de 8 seriam necessárias fazer no máximo 4 comparações. A quantidade de operações ainda é O(n).
Como assim complexidade O(n)?
Vamos lá. O Cormen define, em seu livro, que o tempo que um algoritmo roda é em cima de “passos primitivos” (ou operações primitivas) que por simplicidade ele considera todas de mesmo tempo.
Mas… podemos caracterizar de uma outra maneira a complexidade. Não em cima de toda e qualquer operação. Mas sim em cima de uma operação base. E vamos ver como que essa operação base é chamada em termos da quantidade de elementos.
Por exemplo, o Augusto Galego, em um vídeo sobre complexidade (O algoritmo POLÊMICO que QUEBROU a bolha dev), estava a argumentar sobre a complexidade de um algoritmo muito específico, mais ou menos assim:
function replyThanks(prompt) {
if (prompt === "obrigado") {
return "de nada";
} else if (prompt === "thank you") {
return "you are welcome";
} else if (prompt === "gracias") {
return "¡De nada!";
} ... /* +151 idiomas */
}
Para as demais linguagens. O argumento do Galego é:
- essa função é O(1) porque não tem nada no input que faça crescer a quantidade de operações sendo realizadas além de uma constante
Qual operação ele está usando aqui para lidar como sendo constante? Qual o “passo primitivo” que ele está contando? Ele está contando 2 passos aqui:
- desvio de controle, com o
if - comparação de string
Sim, ele está levando em conta comparação de string como uma operação de tempo fixo. Se eu assumir que comparação de string não é minha operação de interesse, posso levar em conta operações de comparação de caracteres. Que agora é dependente do tamanho da entrada.
Mas será que considerar o tamanho da string vai fazer diferença? Bem, vamos lá. A quantidade de comparações, mesmo considerando otimizações de hardware como SSE acaba sendo proporcional ao tamanho das strings.
Mas são dois argumentos que recebe. E a comparação de string vai parar quando
houver divergência. Ou seja, para a operação strcmp(a, b), o pior caso de
execução é quando a e b sejam a mesma palavra, ou quando a é prefixo de
b ou vice-versa. Esses são os piores cenários. E quem limita nesse pior
cenário? A menor palavra.
Portanto, podemos dizer que strcmp(a, b) = O(min(|a|, |b|)).
Agora, como as palavras conhecidas e sendo comparadas são sempre as mesmas,
podemos dizer que existe uma palavra que tem o maior comprimento, que podemos
chamar de max_len. Então, toda comparação será feita com uma palvra chamada
prompt com palavras que tem todas o tamanho máximo |max_len|. Logo, como
vão ser feitas operações de strcmp e ela depende de
O(min(|prompt|, |max_len|)) e max_len não varia, isso significa que existe
um valor constante que, após |prompt| > |max_len|, o algoritmo se torna então
O(min(prompt > max_len|, |max_len|)) = O(|max_len|). Levando em consideração
que se deseja computar em cima de chamadas de comparações de caracteres/SSE,
isso continua sendo um algoritmo de complexidade constante.
Mas… isso não seria dependente da quantidade de palavras usadas para gerar a
cascata de ifs?
Então… o algoritmo usado já tem as palavras. Mas… como que a gente poderia levar em conta essas palavras usadas na geração do algoritmo? Usando higher order functions, ou HoF: uma função que gera outra função.
Temos aqui a função replyThanks. Para gerar essa função, precisamos receber
um mapeamento entre os diversos agradecimentos e a resposta a esse
agradecimento. Por exemplo, posso gerar para 3 idiomas:
// {
// "obrigado": "de nada",
// "gracias": "¡De nada!",
// "thank you": "you are welcome"
// }
function replyThanks(prompt) {
if (prompt === "obrigado") {
return "de nada";
} else if (prompt === "thank you") {
return "you are welcome";
} else if (prompt === "gracias") {
return "¡De nada!";
}
// retorna undefined implicitamente no caso de não haver mapeamento
}
Aqui, precisaríamos de uma função geraReplyThanks que recebe como input o
mapeamento, e devolve a função que dada uma string retorna a resposta ou não
retorna nada.
Ou seja, seria algo mais ou menos assim, em termos de tipos:
type GeraReplyThanks = (mapeamento: {[agradecimento: string]: string}) => ReplyThanks;
type ReplyThanks = (agradecimento: string) => string | undefined;
Nesse caso, a função geraReplyThanks (que é uma entidade do tipo
GeraReplyThanks) recebe o input mapeamento, e aqui vamos assumir que o
tamanho desse input é |mapeamento| = n. Então, após um processamento…
sei lá, oracular, gera uma função que por sua vez é um conjunto de ifs para
achar o mapeamento adequado. Então, aqui, a função gerada, que é um objeto do
tipo ReplyThanks, é da ordem O(n). Ao receber uma palavra prompt
qualquer, serão feitas O(n) chamadas de strcmp.
Mas a função por si só, em comparação ao seu input, vai operar ainda em O(1)
chamadas de strcmp.
Nas balanças
No caso específico das balanças, a operação com as sacolas de moeda é
insignificante. A operação importante é quantas vezes foi feita a pesagem,
quantas chamadas de scale(left: moeda[], right: moeda[]) foram feitas.
Então por isso que, independente de quanto de trabalho seja feito ordenando e arrumando as sacolas de pesagem, eu só levo em consideração as chamadas de pesagens na balança.
No caso, nas duas estratégias pesagens, vou fazer no pior caso ou n-1 usos
da balança para a estratégia mais simples, ou então n/2 usos da balança, para
uma função de complexidade assintótica O(n).
Dividindo pra conquistar
Bem, como a minha balança eu posso colocar mais coisas do que apenas uma moeda de cada lado, que tal botar metade das moedas de um lado? E a outra metade do outro lado?
Se eventualmente tiver uma moeda sobrando, azar, ela fica separada.
Agora temos 3 conjuntos:
- moedas do prato esquerdo
- moedas do prato direito
- a moeda que sobrou
Se por acaso a balança ficar em equilíbrio após essa pesagem, sabemos que a moeda que sobrou é a de peso diferente, mistério resolvido. Agora, e se ela pendeu para um lado? Bem, nesse caso, o lado que levantou é onde tá a moeda mais leve.
Se esse lado tiver apenas uma moeda, achamos ela. Se não, precisamos repetir o processo, dividindo na metade.
E quantas vezes rodaria esse processo? Bem, até o ponto em que fazer a divisão
inteiro por 2 resultasse em 0. Em outras palavras, O(log2 n).
Algoritmicando
Aqui vamos precisar trabalhar com a coleção de moedas nos passos recursivos. Entào a primeira coisa que vou fazer é esvaziar a sacola de moedas em um array:
function sacola2array(sacola: Sacola): Moeda[] {
const result: Moeda[] = [];
while (!sacola.vazio()) {
const moedaEscolhida = sacolaDeMoedas.pegaMoeda();
result.push(moedaEscolhida);
}
return result;
}
Com essa função, podemos agora separar em duas coleções de mesmo tamanho. Vou separar uma função pra isso para poder fazer a recursão:
function achaMoedaMenor(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void): void {
const moedas = sacola2array(sacolaDeMoedas);
achaMoedaMenorFromArray(moedas, scale, callback);
}
function achaMoedaMenorFromArray(moedas: Moeda[], scale: Balanca, callback: (moeda: Moeda) => void): void {
if (moedas.length % 2 == 1) {
// ok, aqui tem um resto
buscaImpar(moedas, scale, callback);
} else {
// perfeitamente par
buscaPar(moedas, scale, callback);
}
}
function buscaPar(moedas: Moeda[], scale: Balanca, callback: (moeda: Moeda) => void): void {
const meio = moedas.length / 2;
const esq = moedas.slice(0, meio)
const dir = moedas.slice(meio, moedas.length)
const resultadoComparacao = scale(esq, dir);
// só vai ter na prática pender pra esquerda ou pra direita
const moedaMenorNesteArray = resultadoComparacao == "DESCEU_ESQUERDA" ? dir: esq;
if (moedaMenorNesteArray.length == 1) {
// tamanho é 1, achamos a moeda menor
callback(moedaMenorNesteArray[0])
return
}
achaMoedaMenorFromArray(moedaMenorNesteAray, scale, callback);
}
function buscaImpar(moedas: Moeda[], scale: Balanca, callback: (moeda: Moeda) => void): void {
const meio = (moedas.length -1)/ 2;
const esq = moedas.slice(0, meio)
const dir = moedas.slice(meio, moedas.length -1)
const moedaQueSobrou = moedas[moedas.length -1]
const resultadoComparacao = scale(esq, dir);
if (resultadoComparacao == "EQUILIBRIO") {
callback(moedaQueSobrou)
return
}
// só vai ter na prática pender pra esquerda ou pra direita
const moedaMenorNesteArray = resultadoComparacao == "DESCEU_ESQUERDA" ? dir: esq;
if (moedaMenorNesteArray.length == 1) {
// tamanho é 1, achamos a moeda menor
callback(moedaMenorNesteArray[0])
return;
}
achaMoedaMenorFromArray(moedaMenorNesteAray, scale, callback);
}
Aqui a gente tá sempre dividindo em dois. Metade das moedas é descartada a cada passo da busca. Sabe o que isso lembra? Uma busca binária!
Vamos pegar um exemplo para ilustrar, onde M é uma moeda de peso normal e m
a moeda mais leve:
M M M m M M M M
(M M M m)(M M M M) # divide ao meio
1 => \________/
M M M m
(M M)(M m) # divide ao meio
2 => \___/
M m
(M)(m) # divide ao meio
3 => *
ACHOU
Tá, mas como melhorar?
Bem, aqui a gente separou em dois conjuntos a serem pesados. E com isso cortamos em 2, com um resto não sendo pesado. E não conseguimos melhorar o que está sendo pesado. Mas… será que podemos melhorar então a parte que não é pesada?
Agora, no lugar de dividir em 2 conjuntos com uma possível sobra, dividimos em 3 conjuntos. 2 desses precisam ter a mesma quantidade. E o quanto mais igual, melhor. Vamos rodar um experimento com 9 elementos só pra ver como funcionaria?
M M M m M M M M M
(M M M)(m M M)(M M M) # divide em 3
1 => \_____/ não pesado
m M M
(m)(M)(M) # divide em 3
2 => *
ACHOU
Hmmm, e se não tivesse pesado diferente? E se desse mesmo peso?
M M M M M M M M m
(M M M)(M M M)(M M m) # divide em 3
1 => \_____/ \_____/ não pesado
(M)(M)(m)
\_/\_/ não pesado
ACHOU
A ideia se mantém. Se pesou igual, o peso diferente está fora. Só que agora o que está fora não é mais um elemento único, é um conjunto.
Vamos fazer aqui assumindo que estamos trabalhando com potências de 3. Para lidar com outros tamanhos a gente já já ajusta:
function achaMoedaMenor(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void): void {
const moedas = sacola2array(sacolaDeMoedas);
achaMoedaMenorFromArray(moedas, scale, callback);
}
function achaMoedaMenorFromArray(moedas: Moeda[], scale: Balanca, callback: (moeda: Moeda) => void): void {
// assumindo que moeda.length é 3^n
const step = moeda.length / 3;
const esq = moedas.slice(0, step);
const dir = moedas.slice(step, step*2);
const restante = moedas.slice(step*2);
const pesagem2colecao = (cmp: Pesada) => {
if (cmp == "DESCEU_ESQUERDA") {
// desceu pra esquerda? resposta tá na direita
return dir.
} else if (cmp == "DESCEU_DIREITA") {
// desceu pra direita? resposta tá na esquerda
return esq;
} else {
// por esgotamenteo aqui é EQUILIBRIO
// se tá no equilíbrio, a resposta tá no restante
return restante
}
}
const resultadoComparacao = scale(esq, dir);
const moedaMenorNesteArray = pesagem2colecao(resultadoComparacao);
if (moedaMenorNesteArray.length == 1) {
callback(moedaMenorNesteArray[0]);
return;
}
achaMoedaMenorFromArray(moedaMenorNesteArray, scale, callback);
}
Ok, agora vamos pro caso… e se os arrays eventualmente não foram potencias perfeitas de 3?
Para isso, meu desejo é que a diferença entre quaisquer duas coleções seja ou 0 ou 1. Então, se o resto da divisão for 0, não tenho nenhum ajuste a fazer. Se for 1, eu coloco esse 1 no conjunto que fica de fora. Agora, se for 2… eu faço de um jeito que o conjunto de fora fique com um a menos. Para isso, o step que foi dado precisa ser adicionado em 1!
O caso de resto 0 já foi dado, de resto 1 não precisa de ajuste, e só preciso ajustar algo no caso de resto 2:
function achaMoedaMenor(sacolaDeMoedas: Sacola, scale: Balanca, callback: (moeda: Moeda) => void): void {
const moedas = sacola2array(sacolaDeMoedas);
achaMoedaMenorFromArray(moedas, scale, callback);
}
function achaMoedaMenorFromArray(moedas: Moeda[], scale: Balanca, callback: (moeda: Moeda) => void): void {
const sobra = moeda.length % 3;
const step = (moeda.length - sobra) / 3 + (sobra == 2? 1: 0);
const esq = moedas.slice(0, step);
const dir = moedas.slice(step, step*2);
const restante = moedas.slice(step*2);
const pesagem2colecao = (cmp: Pesada) => {
if (cmp == "DESCEU_ESQUERDA") {
// desceu pra esquerda? resposta tá na direita
return dir.
} else if (cmp == "DESCEU_DIREITA") {
// desceu pra direita? resposta tá na esquerda
return esq;
} else {
// por esgotamenteo aqui é EQUILIBRIO
// se tá no equilíbrio, a resposta tá no restante
return restante
}
}
const resultadoComparacao = scale(esq, dir);
const moedaMenorNesteArray = pesagem2colecao(resultadoComparacao);
if (moedaMenorNesteArray.length == 1) {
callback(moedaMenorNesteArray[0]);
return;
}
achaMoedaMenorFromArray(moedaMenorNesteArray, scale, callback);
}
E pronto, resolvido!
E aqui como dividimos em 3 até o esgotamento, temos que a complexidade de busca
é O(log3 n). Para 8 moedas, só precisamos de 2 pesagens.
Uma única moeda diferente
Bem, aqui temos pelo menos 3 moedas. Isso é garantido. Afinal, se tivermos apenas duas moedas, isso significa que ou ambas tem o mesmo peso, ou que ambas tem o mesmo peso.
Para o caso de apenas 3 moedas, como faríamos? Se eu simplesmente compara uma única vez não vou ter a visão inteira. Mas, se der o mesmo peso, posso descartar as duas moedas sendo pesadas. Se deu diferença, eu preciso comparar com a moeda de fora.
E se der algo na balança? Bem, vamos fazer os casos para caso ela fique pendendo para a esquerda:
M m M
M m m
Agora eu preciso fazer mais uma pesagem. No caso, vou pesar a moeda da esquerda com a moeda de fora. Que pode me dar duas saída: mesmo peso, portanto a moeda… 2? seria a correta (o caso da primeira linha). Ou então voltar a pesar pra direita, caso da segunda linha, portanto a moeda da esquerda… moeda 1? seria a moeda diferente.
Um raciocínio semelhante se segue caso o resultado da pesagem seja pendente pra direita:
m M m
m M M
Isso pode ser sumarizado no esquema abaixo:
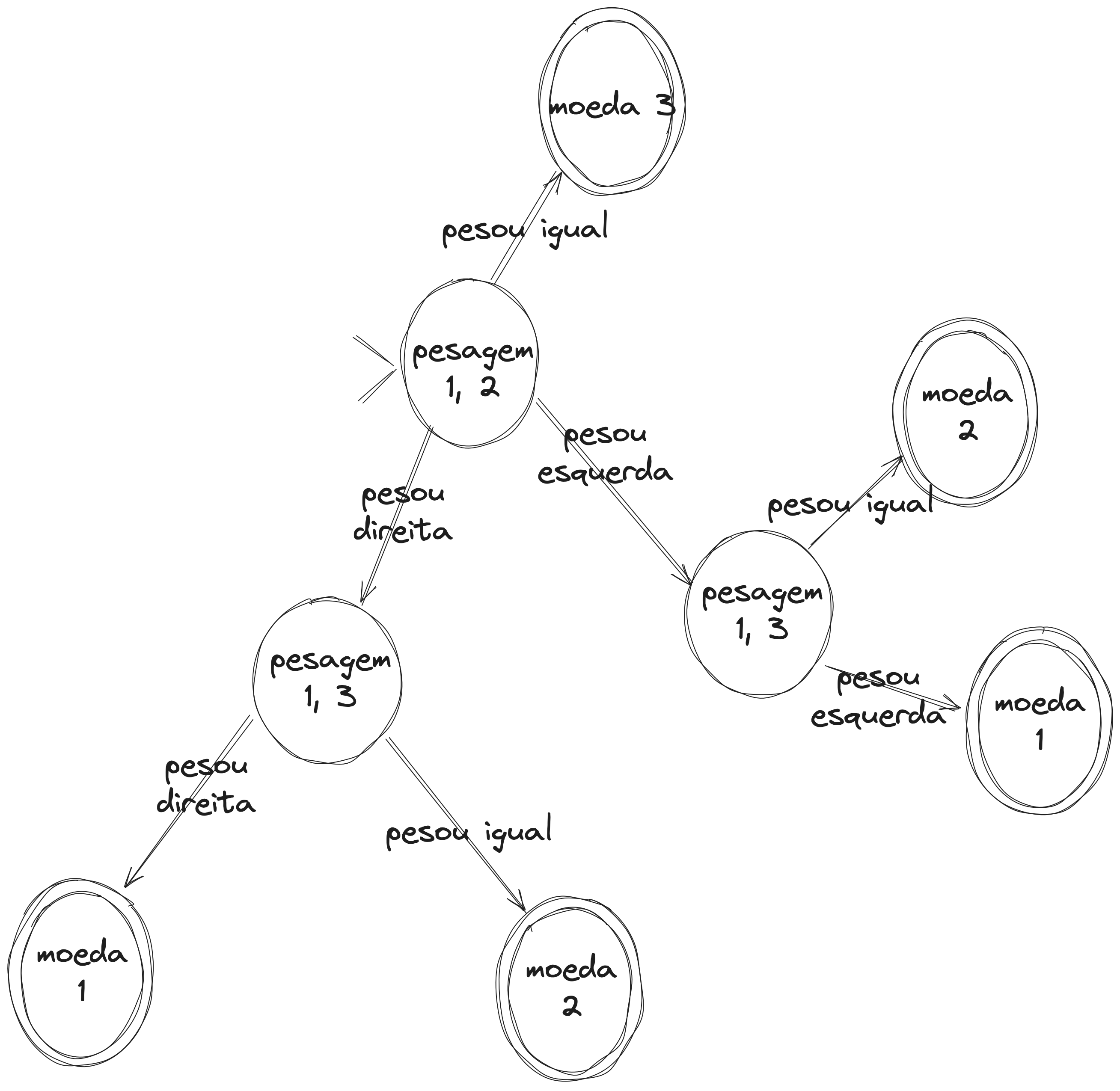
Elaborando uma estratégia
Dá para fazer a estratégia perfeita para detectar em O(log3 n)? Dá. Ela
envolve backtracking. Mas eu vou adaptar a estratégia acima. Vou fazer com o
dobro de pesagens simplesmente para evitar fazer backtracking.
De novo, no mundo perfeito de que a quantidade de moedas é uma potência de 3. Vou usar o mesmo algoritmo acima, mas no lugar de “moeda” na verdade é “conjunto”.
Agora, e se tiver resto? Bem, vamos lá… Diferentemente da alternativa que tentava usar o mínimo de pesagens para achar a moeda necessariamente mais leve, e que portanto tentava deixar os conjuntos de mesmo tamanho, aqui vou fazer questão de deixar o resto separado. Logo, vou ter 4 coleções:
- a primeira, chamada de
c1 - a segunda, chamada de
c2, tem o mesmo tamanho quec1 - a terceira, chamada de
c3, com o mesmo tamanho quec1 - o resto, chamado de
r, que pode ter 1 ou 2
As possíveis distribuições de moedas são as seguintes:
M M M m
M M m M
M m M M
m M M M
m m m M
m m M m
m M m m
M m m m
As colunas representam, respectivamente, c1, c2, c3 e r. As primeiras 4
linhas representam a existência de uma moeda de peso menor, e em qual coleção
ela está. As últimas 4 linhas representam a existência de uma moeda de peso
maior, e em qual coleção ela está.
Agora, vamos às situações: ao pesar c1 e c2, deu igual. O que faço? Sigo
adiante com c3 e r. As linhas que representam c1 e c2 pesarem igual
são:
M M M m
M M m M
m m m M
m m M m
Como se pode ver, a moeda diferente estará necessariamente ou em c3 ou em
r. Mas… bem, isso traz um problema. Se |c3 + r| for 2? Isto é, caso o
tamanho de c3 for 1 e o tamanho do resto também for 1? Nessa situação,
pegamos uma moeda de origem conhecida que seria descartada, por exemplo a
primeira moeda de c1. E quando isso acontece? Bem, quando a quantidade de
moedas a ser pesada é 4.
Agora, se pender para a esquerda, já sabemos que o elemento distinto ou está em
c1 ou em c2. Portanto, nessa situação, r já pode ser esquecido. As
situações que pendem para a esquerda são:
M m M M
M m m m
Sigo o algoritmo de escolha com a pesagem de c1 com c3.
Se lembra que falei que talvez faltassem elementos para determinar com
certeza em qual coleção estaria? Bem, essa situação só acontece de o tamanho de
c1 for 2, o que significa que o vetor tinha tamanho 7 ou 8. Se c1 tiver
exatamente 1 elemento, tá tudo resolvido já. Mas nesse caso de ter 2,
precisamos importar um elemento faltante. De onde vou pegar esse elemento?
Posso pegar do primeiro elemento do resto.
E para os casos sem resto? Em tese, os possíveis casos são:
M M m
M m M
m M M
m m M
m M m
M m m
Mas como lidamos caso a coleção que vai ser passada para frente tenha apenas 2 elementos? Bem, sabendo qual coleção é essa, eu pego o primeiro elemento de uma coleção que seria descartada.