Usando Java moderno para fazer aritmética de Peano
Sabia que em Java dá para fazer destructuring de records? E que isso permite
junto a sealed interface fazer uns pattern-matchings bem legais? Pois vamos
explorar isso!
Desestruturando records
Peguemos um record bem simples. Que tal, Coord?
public record Coord(double x, double y) {}
Muito bem, isso está bom o suficiente. Agora, vamos dizer que queremos saber o
ângulo que esse esse ponto faz em relação a origem. E também vamos assumir que
receberemos um objeto desconhecido, que devemos retornar 0 exceto caso ele
seja um Coord.
Tá, mas como que calcula esse ângulo? Eu posso pegar uma operação matemática
arc sin(t) e calcular. Mas como sin e cos dependem do valor da
hipotenusa, e eu tenho aqui apenas o par ordenado, eu posso lidar com isso não
através do arc sin ou arc cos, mas através do arc tan. Por quê? Bem,
nessas operações trigonométricas reversas, eu preciso fornecer o sin(t) para
em cima disso obter o t, afinal a definição de arc sin é derivada disso:
arc sin(sin(t)) = t. E eu teria alguns níveis de dificuldades para obter a
partir do ponto o seno que faria o ângulo entre o eixo x indo pra direta e a
reta que passa pela origem e por esse ponto específico.
Pulando a questão das identidades trigonométricas, eu tenho que o valor da
tangente de um ângulo em um triângulo retângulo é “cateto oposto/cateto
adjacente”. Em relação a esse ângulo específico que procuro, o “cateto oposto”
dele é numericamente igual ao valor c.y da coordenada c, e o “cateto
adjacente” é numericamente igual ao valor c.x. Então basta fazer a divisão
c.y/c.x, certo?
Na real, pegar o valor de arc tan a partir de coordenadas é tão comum que até
simplificaram isso! Criaram uma função “2”: arc tan2(y, x) : t. Em Java, ela
reside em Math.atan2(double y, double x). E também tem na biblioteca
matemática de diversas linguagens, de tão comum operação que é.
Para isso, uma das alternativas é verificar a instância:
public static double anguloOrigem(Object o) {
if (o instanceof Coord) {
Coord c = (Coord) o;
return Math.atan2(c.y(), c.x());
}
return 0;
}
Isso está mais a par com um estilo Java de programar antes do Java 14. Mas,
vamos ser sinceros, estamos usando Java moderno! Inclusive records que veio
depois do Java 14. Podemos melhorar isso usando o instanceof aprimorado
(vide JEP 394):
public static double anguloOrigem(Object o) {
if (o instanceof Coord c) {
return Math.atan2(c.y(), c.x());
}
return 0;
}
Ok, isso já melhorou. Mas eu preciso em algum momento da coordenada c? Na
real? Não mesmo. Eu preciso apenas do par ordenado: x,y. E a partir do Java
21 (JEP 440) eu posso obter apenas isso! Sem
precisar mais da variável c:
public static double anguloOrigem(Object o) {
if (o instanceof Coord(double x, double y)) {
return Math.atan2(y, x);
}
return 0;
}
E podemos ser mais ousados: podemos neste contexto usar var:
public static double anguloOrigem(Object o) {
if (o instanceof Coord(var x, var y)) {
return Math.atan2(y, x);
}
return 0;
}
Muito bem, se eu por pra imprimir para, por exemplo,
System.out.prinln(new Coord(5, 5)), eu vou obter um número bem estranho:
0.7853981.... Mas, por quê? Esse ângulo deveria dar 45º…
Ah! Math.atan2 e as outras operações de arco-função trigonométrica retorna o
ângulo em radianos! Preciso transformar em graus se quiser ler de modo
convencional. Como em uma volta completa temos 360º ou 2 pi rad, isso significa
que pegar um ângulo t em radianos eu consigo transformar para graus dividindo
por 2 pi (isso significa que eu deixa de medir em radianos e passo a medir em
“fração da volta”) e multiplico por 360 (que deixaria de ser “fração da volta”
e passa a ser “graus”) eu passo a ter o valor mais usual.
Uma pequena análise dimensional:
Beleza, faz sentido. As unidades batem e só fica graus. Como multiplicar por
360 e logo em seguida dividir por 2pi é redundante, podemos simplificar o fator
comum 2 e ficar com multiplicar por 180 e dividir por pi.
Então eu posso fazer isso:
System.out.println(calculaAngulo(new Coord(5, 5)) * 180/Math.PI);
E tudo maravilha! Obtenho o 45 que eu estava esperando.
Pattern matching com sealed interface
Uma das maravilhas do Java moderno foram as sealed interfaces. Basicamente,
com uma sealed interface, você precisa declarar na interface “selada” (selada
no sentido de “selo”, de que após passar o selo não se abre mais) quem a
implementa. Ou então você pode até omitir quem implementa, desde que a
interface e suas implementações estejam no mesmo arquivo.
Um exemplo quando estão declarados juntos:
public sealed interface Fruta {
public final class Abacate implements Fruta {
void cabelo() {
System.out.println("faz bem pro cabelo");
}
}
public final class Abobora implements Fruta {
void susto() {
System.out.println("abóboras são de halloween");
}
}
public final class Jerimum implements Fruta {
void nhami() {
System.out.println("hmm, jerimum, nhami nhami");
}
}
}
Ou então, caso estejam em arquivos distintos:
public sealed interface Fruta
permits Abacate, Abobora, Jerimum {
}
Nota: as classes não sofreram mudanças, apenas o
permitsdasealed interfaceque foi afetado.
Agora, o que isso permite? Bem, permite fazer uma busca exaustiva no switch
pelas implementações da interface:
static void print(Fruta f) {
switch (f) {
case Abacate a -> a.cabelo();
case Abobora a -> a.susto();
case Jerimum j -> j.nhami();
case null -> System.out.println("nulo");
}
}
Notou algo interessante? Ausência de default? Pois bem, estou usando uma
interface selada, então eu sempre tenho conhecimento de todas as implementações
daquela interface. Então eu tenho uma quantidade finita de casos nos quais eu
preciso conferir para cobrir com totalidade.
Se houver outra implementação de Fruta, esse switch passa a falhar na
compilação. E uma coisa interessante é que o caso null é opcional, mas muda a
semântica:
- se tiver um
case null, ele assume que a variável possa ter o valornulo - caso contrário, assume-se que essa variável nunca será nula nesse trecho
Por exemplo, o código a seguir também é válido:
static void printNonNull(Fruta f) {
switch (f) {
case Abacate a -> a.cabelo();
case Abobora a -> a.susto();
case Jerimum j -> j.nhami();
}
}
A diferença está ao chamar passando como parâmetro null. Na função print,
simplesmente chamamos o ramo case null, o que significa imprimir nulo. Já
na função printNonNull, dá um NullPointerException, pois semanticamente não
deveria ter nulo nesse trecho (inclusive o IntelliJ aponta o warning).
Um exemplo não tão pequeno como eu esperava: Optional reimaginado
Vamos reimaginar o que é a mônada Optional do Java, introduzida no Java 8.
Para começar, que tal tratar ela por um nome mais… comum?, no mundo de
mônadas? Que tal ser Maybe?
Vamos definir o tipo Maybe<T>, que por sua vez pode ser None (na ausência
do valor) ou Just<T> (na presença). Se eu precisar resgatar um valor, eu só
posso fazer operações típicas de pattern-matching:
final Maybe<String> valor = someValue();
final var qtdChars = valor.map(String::length);
System.out.println("Tamanho da string? " + switch (qtdChars) {
case Just(var x) -> x;
case None<?> unused -> "sem tamanho";
});
Ficou bacana, né? Eu começo com uma Maybe<String>, então transformo em uma
Maybe<Integer> e com isso obtenho finalmente algo para escrever, e para obter
esse valor eu preciso percorrer ambos os branches de processamento: Just e
None. Eu posso prosseguir também com curso de processamento:
final Maybe<String> valor = someValue();
switch (valor) {
case Just(var s) -> saveToDatabase(s);
case None<?> unused -> System.out.println("Não salvando nada porque não passou nada");
}
Legal. Com essa ideia geral (em breve entro nos detalhes) eu consigo
implementar o safe head descrito
neste post sobre Haskell,
um post que procura explorar a implementação da mônada Maybe<T>.
Mas antes de entrar nos detalhes do Maybe<T>, vamos precisar definir um jeito
de lidar com listas. Se eu usar a interface do Java, não vou ter acesso tão
simples ao car/cdr da lista, não pelo menos que dê para usar em
pattern-matching.
Essa parte deste post acaba tendo um overlap com o post Criando filas e pilhas “apenas” com funções em java, mas a leitura desse outro não é mandatória para entender este daqui.
Bem, então vou definir aqui, List<T>. Vai ser uma sealed interface, com as
implementações record Empty<T>() implements List<T> {} e
record ValuedList<T>(T car, List<T> cdr) implements List<T> {}. E, sim, não
preciso de métodos. Mas seria interessante ter uma opção de construir. E
também interessante evitar múltiplas instâncias de um List.Empty, porque como
tem valor é seguro usar o mesmo objeto para List.Empty<String> e para
List.Empty<List<Maybe<T>>>.
Já posso criar com empty(), lista com um único elemento e um começo de
indício para uma lista com múltiplos elementos:
public sealed interface List<T> {
record Empty<T>() implements List<T> {
private static final Empty<Object> INSTANCE = new Empty<>();
}
record ValuedList<T>(T car, List<T> cdr) implements List<T> {}
static <T> Empty<T> empty() {
return (Empty<T>) Empty.INSTANCE;
}
static <T> ValuedList<T> single(T t) {
return new ValuedList<>(t, empty());
}
static <T> List<T> of(T ...elements) {
return // mistério...
}
}
Como eu não posso usar destructuring em arrays java, preciso de uma estratégia mais elaborada.
A propósito, o tipo do objeto em uma ellipsis é array daquele tipo, portanto aqui
elementsda funçãoList.oftem tipoT[]. A diferença não está no tipo dessa variável, mas sim na assinatura da função, que passa a aceitar múltiplos elementos. Portanto posso chamarList.of("a", "b", "c")sem problemas pois quem chama sabe que é uma ellipsis.
Então, como posso fazer isso? Uma estratégia seria usar iteração simples para resolver o problema, mas aí perde a graça da programação funcional. Eu não posso iterar de modo clássico, mas posso iterar através de uma função de cauda! Uma recursão em função de cauda mais especificamente. Vide Trampolim, exemplo em Java, em que eu falo sobre funções de cauda com um pouco mais de carinho.
Mas em resumo: se eu tenho uma coleção T indexada, eu posso passar para
frente da função o valor acumulado (na primeira chamada é o elemento neutro),
o índice da iteração atual (na primeira chamada é 0, ou equivalente) e a
coleção. A chamada recursiva vai passar uma acumulação baseada em T[idx] e a
acumulação anterior, o próximo índice e a coleção novamente.
Para o caso da lista, qual o caso base? A lista empty(), claro. Como a lista
foi criada pensando em car | cdr, vou iterando do fim pro começo, então o
primeiro índice será o tamanho da coleção menos 1, saindo ao chegar no índice
com posição negativa. Ou seja, vou ter essa chamada aqui:
static <T> List<T> of(T ...elements) {
return build(elements, elements.length - 1, empty());
}
static <T> List<T> build(T[] elements, int cur, List<T> prev) {
if (cur < 0) {
return prev; // retorna o que foi acumulado até o momento
}
// desenvolvendo ainda
}
Toda computação precisa ser feita antes da chamada recursiva. Ou seja, nos
parâmetros passados para a função. Então necessariamente o passo recursivo será
return build(...);, com o segredo nos parâmetros.
Já discutimos brevemente o que vou passar, né? A coleção, o próximo índice, e a acumulação:
static <T> List<T> of(T ...elements) {
return build(elements, elements.length - 1, empty());
}
static <T> List<T> build(T[] elements, int cur, List<T> prev) {
if (cur < 0) {
return prev;
}
return build(elements, cur - 1, /* algo com prev e elements[cur] */);
}
Ok, agora eu preciso criar uma lista que tenha como cabeça elements[cur] e
como cauda prev! Basicamente new ValuedList<>(elements[cur], prev),
inclusive poderia usar isso. Mas não parece tão elegante, então vou criar uma
função auxiliar chamada prepend que passo os elementos, e ela cuida dos
detalhes internos:
static <T> ValuedList<T> prepend(T t, List<T> l) {
return new ValuedList<>(t, l);
}
static <T> List<T> build(T[] elements, int cur, List<T> prev) {
if (cur < 0) {
return prev;
}
return build(elements, cur - 1, prepend(elements[cur], prev));
}
Pronto. Agora só colocando algumas anotações para suprimir alguns warnigns que são seguros ignorar:
public sealed interface List<T> {
record Empty<T>() implements List<T> {
private static final Empty<Object> INSTANCE = new Empty<>();
}
record ValuedList<T>(T car, List<T> cdr) implements List<T> {}
@SuppressWarnings("unchecked")
static <T> Empty<T> empty() {
return (Empty<T>) Empty.INSTANCE;
}
static <T> ValuedList<T> single(T t) {
return new ValuedList<>(t, empty());
}
static <T> ValuedList<T> prepend(T t, List<T> l) {
return new ValuedList<>(t, l);
}
@SafeVarargs
static <T> List<T> of(T ...elements) {
return build(elements, elements.length - 1, empty());
}
static <T> List<T> build(T[] elements, int cur, List<T> prev) {
if (cur < 0) {
return prev;
}
return build(elements, cur - 1, prepend(elements[cur], prev));
}
}
Muito bem, vamos testar?
System.out.println(List.of("a", "b", "c"));
// ValuedList[car=a, cdr=ValuedList[car=b, cdr=ValuedList[car=c, cdr=Empty[]]]]
System.out.println(List.of());
// Empty[]
Funcionou! Beleza, agora vamos começar os trabalhos? Ainda sem me preocupar com
os detalhes de como funcionam as coisas em Maybe<T>. Vamos fazer uma redução?
Para este caso específico, vou pegar o reduce como retornando o mesmo tipo
da lista. Algo assim: T[] -reducer-> T. Mas… bem, talvez a lista esteja
vazia. Então nesse caso eu não retornaria nada. Como codificar isso? Retornando
um Maybe<T>! T[] -reducer-> Maybe<T>!
Eu passei por várias implementações e deadends, mas a melhor versão foi me
preparar para processar com pattern-matching, como por exemplo retornar None
para a lista vazia:
static <T> Maybe.None<T> reduce(BinaryOperator<T> reducer, List.Empty<T> e) {
return Maybe.none();
}
Mas só definir os tipos da interface selada não satisfaz o java. Por exemplo, esse código não compila:
static <T> Maybe.None<T> reduce(BinaryOperator<T> reducer, List.Empty<T> e) {
return Maybe.none();
}
static <T> Maybe.Just<T> reduce(BinaryOperator<T> reducer, List.ValuedList<T> l) {
// apenas um stub, não leve a sério
return Maybe.just(l.car());
}
final List<String> l = List.of("a", "b", "c");
final Maybe<String> concat = reduce(String::concat, l);
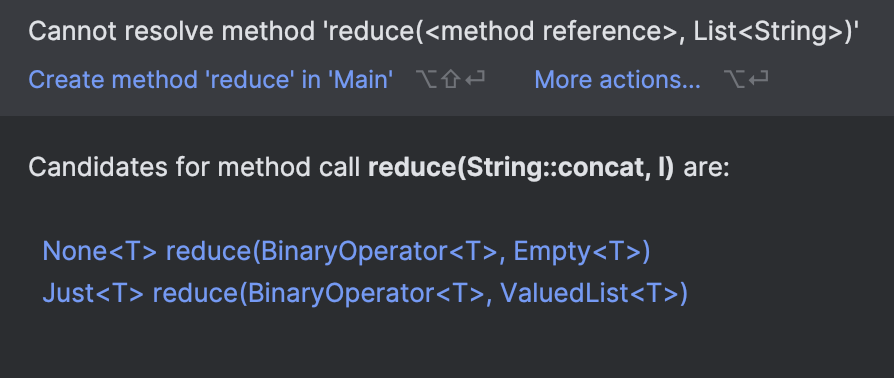
Então minha solução foi criar um método de entrada:
static <T> Maybe.None<T> reduce(BinaryOperator<T> reducer, List.Empty<T> e) {
return Maybe.none();
}
static <T> Maybe.Just<T> reduce(BinaryOperator<T> reducer, List.ValuedList<T> l) {
// apenas um stub, não leve a sério
return Maybe.just(l.car());
}
static <T> Maybe<T> reduce(BinaryOperator<T> reducer, List<T> l) {
return switch (l) {
case List.ValuedList<T> valuedList-> reduce(reducer, valuedList);
case List.Empty<T> empty -> reduce(reducer, empty);
};
}
final List<String> l = List.of("a", "b", "c");
final Maybe<String> concat = reduce(String::concat, l);
E agora obviamente que falhou no stub: Just[r=a]. Preciso agora resolver a
questão de como computar o reduce. Bem, vamos lá. Tenho uma lista que tem
pelo menos um elemento. Se tiver apenas esse único elemento, retorno
just(t.car). Caso contrário, vou precisar o tail e então chamar o redutor
para car e reduce(reducer, tail).
static <T> Maybe.Just<T> reduce(BinaryOperator<T> reducer, List.ValuedList<T> l) {
return switch (l.cdr()) {
case List.ValuedList<T> valuedTail -> Maybe.just(reducer.apply(l.car(), reduce(reducer, valuedTail).r()));
case List.Empty<?> unused -> Maybe.just(l.car());
};
}
E magia! Agora, e se eu detectasse logo de cara na entrada que quando eu tenho uma lista com apenas um elemento eu posso só retornar ele? Eu posso aplicar destructuring de records!
static <T> Maybe<T> reduce(BinaryOperator<T> reducer, List<T> l) {
return switch (l) {
case List.ValuedList<T>(var head, List.Empty<?> empty) -> Maybe.just(head);
case List.ValuedList<T> valuedList-> reduce(reducer, valuedList);
case List.Empty<T> empty -> reduce(reducer, empty);
};
}
Necessidade para isso? Nenhuma, apenas mostrar a possibilidade mesmo. Agora eu consigo verificar se algumas coisinhas estão corretas:
final List<String> l = List.of("a", "b", "c");
System.out.println(reduce((a, b) -> a + "," + b, l));
// Just[r=a,b,c]
System.out.println(reduce((a, b) -> a + "," + b, List.of("único")));
// Just[r=único]
System.out.println(reduce((a, b) -> a + "," + b, List.of()));
// None[]
Tudo em ordem. Temos redução.
Mas eu estou pela mônada Maybe<T>, a redução foi só um good to have. Como
seguir com isso? Vamos agora implementar o head. Como funciona? Bem, se a
lista tiver elementos, retorna um just do primeiro elemento, caso contrário
retorna um none. De novo, o padrão de func(Sealed) return switch case Impl
impl func(impl) funciona e muito bem. Vamos usar esse padrão!
static <T> Maybe.None<T> head(List.Empty<T> l) {
return Maybe.none();
}
static <T> Maybe.Just<T> head(List.ValuedList<T> l) {
return Maybe.just(l.car());
}
static <T> Maybe<T> head(List<T> l) {
return switch (l) {
case List.ValuedList<T> valued -> head(valued);
case List.Empty<T> empty -> head(empty);
};
}
Nesse caso… foi overkill mesmo… ou será que não? Na real vai depender de
como vai ser feita a concatenação de chamadas de funções. Por exemplo, posso
alterar uma coisinha no List.of:
@SafeVarargs
static <T> ValuedList<T> of(T head, T ...elements) {
return build(head, elements, elements.length - 1, empty());
}
static <T> List<T> of(T[] elements) {
return oldBuild(elements, elements.length - 1, empty());
}
static <T> ValuedList<T> of(T element) {
return single(element);
}
static <T> Empty<T> of() {
return empty();
}
static <T> ValuedList<T> build(T head, T[] elements, int cur, List<T> prev) {
if (cur < 0) {
return prepend(head, prev);
}
return build(head, elements, cur - 1, prepend(elements[cur], prev));
}
static <T> List<T> oldBuild(T[] elements, int cur, List<T> prev) {
if (cur < 0) {
return prev;
}
return oldBuild(elements, cur - 1, prepend(elements[cur], prev));
}
Aqui eu destrinchei o of. Existem situações em que ele vai retornar
necessariamente uma lista com valores (quando passa 1 ou mais argumentos),
ou talvez uma lista vazia. Fiz isso assim:
static <T> Empty<T> of(); // implementação
static <T> ValuedList<T> of(T element); // implementação
static <T> ValuedList<T> of(T head, T ...elements); // implementação
No caso do varargs, eu cuidei para garantir pelo menos a existência do head,
assim quem quiser usar com varargs necessariamente vai obter como resultado um
ValuedList. Se eu tivesse deixado o varargs sem o head, apesar de que nos
cenários em que o programador usa a função preenchendo com valores que ele
controla individualmente, existem situações plausíveis de que ele receba um
array e passe para a função, logo até mesmo um array vazio. Para esse tipo de
situação eu tratei forçando a existência do head fora do varargs.
Mas para cobrir o caso de passar como argumento um único array, criei também uma função específica para isso:
static <T> List<T> of(T[] elements); // implementação
Eu posso retornar empty, afinal o array pode ter comprimento 0. Nota que
para o of(T[]) eu deixei a função auxiliar build original (agora renomeada
para oldBuild). E como eu precisava garantir que a build chamada para
of(T, T...) retornasse um ValuedList, fiz uns ajustes para no último passo
colocar o head na frente do acumulado.
E com essa brincadeira posso fazer isso:
System.out.println(head(List.of("a", "b", "c")).r());
// a
Que imprime corretamente. Algo que eu não teria caso eu implementasse apenas
assim (sem as implementações para head(ValuedList) e head(Empty)):
static <T> Maybe<T> head(List<T> l) {
return switch (l) {
case List.ValuedList(var h, var t) -> Maybe.just(h);
case List.Empty<T> empty -> Maybe.none();
};
}
Então, em algum momento dos meus primeiros rascunho fez sentido pleno separar essa questão de tipo da lista. Infelizmente o rascunho original foi perdido, então me resta apenas imaginar o tipo de ação que eu teria feito.
Finalmente, tudo isso para quê? Bem, o desafio da mônada Maybe era para pegar
o terceiro elemento de uma lista. E como fazemos? Puxando a notação Haskell:
thirdElement :: [a] -> Maybe a
thirdElement xs =
myTail xs >>= a ->
myTail a >>= b ->
myHead b
Que seria algo assim em uma leitura mais Java:
myTail(xs)
.bind(a -> myTail(a))
.bind(b -> myHead(b))
Tem uma notação que o post sobre Haskell que usa a
do-notation, mas que achei que não cabia para o que eu queria passar o sentimento aqui.
Ou seja: tail tail head. Temos o retorno Maybe<T>. Mônadas precisam ter em
si a operação bind, que no caso do Optional do Java é o flatMap (mais
detalhes aqui no
Tutorials Point).
Como a minha ideia com o Maybe<T> é reimaginar Optional<T>, vamos manter a
operação flatMap (ainda a implementar) e adicionar o método bind:
public sealed interface Maybe<R> {
static <R> Just<R> just(R value) {
return new Just<>(Objects.requireNonNull(value));
}
@SuppressWarnings("unchecked")
static <X> None<X> none() {
return (None<X>) None.INSTANCE;
}
static <R> Maybe<R> of(R value) {
if (value == null) {
return none();
}
return just(value);
}
record Just<R>(R r) implements Maybe<R> {
// flatMap...
}
record None<R>() implements Maybe<R> {
static final None<Object> INSTANCE = new None<>();
// flatMap...
}
default <T> Maybe<T> bind(Function<R, Maybe<T>> mapper) {
return flatMap(mapper);
}
<T> Maybe<T> flatMap(Function<R, Maybe<T>> mapper);
}
Beleza, vamos abstrair novamente o Maybe só mais um pouquinho! E vamos fingir
que bind está funcionando adequadamente. Como pegar o terceiro elemento de um
List<T>?
static <T> Maybe<T> thirdElement(List<T> l) {
return tail(l).bind(Main::tail).bind(Main::head);
}
System.out.println(thirdElement(List.of("a", "b", "c", "d")));
// Just[r=c]
System.out.println(thirdElement(List.of("a", "b", "c")));
// Just[r=c]
System.out.println(thirdElement(List.of("a", "b")));
// None[]
System.out.println(thirdElement(List.of("a")));
// None[]
System.out.println(thirdElement(List.of()));
// None[]
Perfeito! Tudo funcionando perfeitamente no mundo da Hipotesilândia! Agora
finalmente posso voltar a falar da implementaçõa em Java da mônada Maybe<T>,
para ser uma versão reimaginada de Optional<T>.
Além do flatMap, outras funções úteis são:
filermapor
O stream é interessante também, vale a pena, deixa a escrita mais suave em
uma operação comum.
As opções que acessam o valor interno, como get, isEmpty, orElse,
ifPresentOrElse, tudo não preciso, pois afinal esses métodos são apenas para
inspecionar o valor interno e tomar alguma decisão. Pra isso, prefiro que se
use pattern-matching. Minha API, minhas regras.
Os construtores auxiliares já coloquei. Vamos agora adicionar os métodos novos que preciso implementar ainda:
public sealed interface Maybe<R> {
static <R> Just<R> just(R value) {
return new Just<>(Objects.requireNonNull(value));
}
@SuppressWarnings("unchecked")
static <X> None<X> none() {
return (None<X>) None.INSTANCE;
}
static <R> Maybe<R> of(R value) {
if (value == null) {
return none();
}
return just(value);
}
record Just<R>(R r) implements Maybe<R> {
// flatMap map filter or stream...
}
record None<R>() implements Maybe<R> {
static final None<Object> INSTANCE = new None<>();
// flatMap map filter or stream...
}
default <T> Maybe<T> bind(Function<R, Maybe<T>> mapper) {
return flatMap(mapper);
}
<T> Maybe<T> flatMap(Function<R, Maybe<T>> mapper);
<T> Maybe<T> map(Function<R, T> mapper);
Maybe<R> filter(Predicate<R> filter);
Maybe<R> or(Supplier<Maybe<R>> supplier);
Stream<R> stream();
}
Bem, bora lá? No caso do None, as operações flatMap, map, filter são
todas no-op (retornam this). Então já podemos até implementar:
@SuppressWarnings("unchecked")
record None<R>() implements Maybe<R> {
static final None<Object> INSTANCE = new None<>();
@Override
public <T> None<T> map(Function<R, T> mapper) {
return (None<T>) this;
}
@Override
public None<R> filter(Predicate<R> cond) {
return this;
}
@Override
public <T> None<T> flatMap(Function<R, Maybe<T>> mapper) {
return (None<T>) this;
}
// or stream...
}
Só faltaram os método or e stream. No caso do or, eu vou pegar o
resultado gerado pelo supplier. E para a stream eu retorno a stream vazia:
@SuppressWarnings("unchecked")
record None<R>() implements Maybe<R> {
static final None<Object> INSTANCE = new None<>();
@Override
public <T> None<T> map(Function<R, T> mapper) {
return (None<T>) this;
}
@Override
public None<R> filter(Predicate<R> cond) {
return this;
}
@Override
public <T> None<T> flatMap(Function<R, Maybe<T>> mapper) {
return (None<T>) this;
}
@Override
public Maybe<R> or(Supplier<Maybe<R>> supplier) {
return supplier.get();
}
@Override
public Stream<R> stream() {
return Stream.empty();
}
}
Pronto. Agora, o mesmo para Just. Começar com or, que é no-op (retornando
this), e stream que é retornar o elemento dele em Stream:
record Just<R>(R r) implements Maybe<R> {
@Override
public Stream<R> stream() {
return Stream.of(r);
}
@Override
public Just<R> or(Supplier<Maybe<R>> supplier) {
return this;
}
// flatMap map filter ...
}
flatMap vai ser basicamente chamar a função com o valor, e map eu preciso
envolver o resultado da função. Já filter eu mantenho o tipo porém posso devo
retornar None caso a condição não seja atendida:
record Just<R>(R r) implements Maybe<R> {
@Override
public Stream<T> stream() {
return Stream.of(r);
}
@Override
public Just<R> or(Supplier<Maybe<R>> supplier) {
return this;
}
@Override
public <T> Maybe<T> map(Function<R, T> mapper) {
return Maybe.of(mapper.apply(r));
}
@Override
public Maybe<R> filter(Predicate<R> cond) {
if (cond.negate().test(r)) {
return Maybe.none();
}
return this;
}
@Override
public <T> Maybe<T> flatMap(Function<R, Maybe<T>> mapper) {
return mapper.apply(r);
}
}
E caso queria recuperar o valor? Só fazer pattern-mathing!
final Maybe<String> valor = Maybe.none();
final var qtdChars = valor.map(String::length);
System.out.println("Tamanho da string? " + switch (qtdChars) {
case Just(var x) -> x;
case None<?> unused -> "sem tamanho";
});
// Tamanho da string? sem tamanho
final Maybe<String> valor = Maybe.just("jeff");
final var qtdChars = valor.map(String::length);
System.out.println("Tamanho da string? " + switch (qtdChars) {
case Just(var x) -> x;
case None<?> unused -> "sem tamanho";
});
// Tamanho da string? 4
switch-case-when
Mais um ponto sobre Java moderno: o switch-expression agora aceita o when!
Por exemplo, vamos pegar o perímetro de uma forma:
static Valor perimetro(Object o) {
return switch (o) {
case Retangulo(var a, var b) -> // a + b;
case Diamante(var a, var b) -> // sqrt(a^2 + b^2)*4;
case Elipse(var a, var b) -> // algo entre 4*a + 4*b e sqrt(a^2 + b^2)*4;
default -> // inválido;
}
}
Primeiro, vamos encodar Valor? Temos aqui 3 tipos distintos:
- um valor exato
- um valor entre 2, sem precisão
- um valor inválido
Usando sealed interfaces:
public sealed interface Valor {
record Invalido() implements Valor {}
record Exato(double v) implements Valor {}
record Range(double min, double max) implements Valor {}
}
E, sim, não há valor exato para o tamaho de uma elipse genérica. Mas, e se a elipse passada for um círculo? Aí temos um vamos exato conhecido! Que seria 2 pi!
Vamos primeiro implementar sem o círculo, para depois verificar a implementação levando em conta o círculo:
public sealed interface Valor {
record Invalido() implements Valor {
static final Invalido INSTANCE = new Invalido();
}
record Exato(double v) implements Valor {}
record Range(double min, double max) implements Valor {}
record Elipse(double a, double b) {}
record Diamante(double a, double b) {}
record Retangulo(double a, double b) {}
static Valor perimetro(Object o) {
return switch (o) {
case Elipse(var a, var b) -> new Range(Math.sqrt(a*a + b*b) * 4, 4*a + 4*b);
case Diamante(var a, var b) -> new Exato(Math.sqrt(a*a + b*b) * 4);
case Retangulo(var a, var b) -> new Exato((a+b)*2);
default -> Invalido.INSTANCE;
};
}
public static void main(String[] args) {
System.out.println(new Elipse(5, 5));
// Range[min=40.0, max=28.284271247461902]
System.out.println(perimetro(new Diamante(5, 5)));
// Exato[v=28.284271247461902]
System.out.println(perimetro(new Retangulo(10, 10)));
// Exato[v=40.0]
}
}
Bem, eu primeiro peguei o range do perímetro da elipse com base nas
aproximações do losango/diamante e do retêngulo: o losango cabe dentro da
elipse (está inscrito), portanto é um limite inferior, e o retângulo já envolve
a elipse por fora (circumscreve), um limite superior. Além desses limites,
posso limitar no perímetro do círculo inscrito de raio menor(a,b) e do
círculo circunscrito de raio maior(a,b). Para isso, preciso adaptar Range:
adicionar o método para restringir o mínimo e para restringir o máximo.
record Range(double min, double max) implements Valor {
Range restringirMin(double min2) {
if (min2 > min) {
return new Range(min2, max);
}
return this;
}
Range restringirMax(double max2) {
if (max2 < max) {
return new Range(min, max2);
}
return this;
}
}
E agora adaptando o cálculo do perímetro:
static Valor perimetro(Object o) {
return switch (o) {
case Elipse(var a, var b) -> new Range(Math.sqrt(a*a + b*b) * 4, 4*a + 4*b)
.restringirMin(2*Math.PI*a)
.restringirMax(2*Math.PI*b);
case Diamante(var a, var b) -> new Exato(Math.sqrt(a*a + b*b) * 4);
case Retangulo(var a, var b) -> new Exato((a+b)*2);
default -> Invalido.INSTANCE;
};
}
System.out.println(perimetro(new Elipse(5, 5)));
// Range[min=31.41592653589793, max=31.41592653589793]
System.out.println(perimetro(new Diamante(5, 5)));
// Exato[v=28.284271247461902]
System.out.println(perimetro(new Retangulo(10, 10)));
// Exato[v=40.0]
Show, com os mesmos lados saiu com um intervalo único de valores! mas, pera…
fiz uma besteira. O que acontece se for passado a > b? Era pra chamar aquela
função de max(a, b) e min(a, b) para restringir os maiores e menores
valores, não? Na verdade… podemos garantir isso. Sabe como? Transformando a
elipse. E não dentro do case Elipse(var a, var b), não não não. Deixa ele do
jeito que está… vamos fazer um caso especial, que recebo
Elipse(var b, var a) e retorno o perímetro para
perimetro(new Elipse(a, b))! Como fazer isso? Adicionando uma clásula when
ao switch-case!
static Valor perimetro(Object o) {
return switch (o) {
case Elipse(var b, var a) when a < b -> perimetro(new Elipse(a, b));
case Elipse(var a, var b) -> new Range(Math.sqrt(a*a + b*b) * 4, 4*a + 4*b)
.restringirMin(2*Math.PI*a)
.restringirMax(2*Math.PI*b);
case Diamante(var a, var b) -> new Exato(Math.sqrt(a*a + b*b) * 4);
case Retangulo(var a, var b) -> new Exato((a+b)*2);
default -> Invalido.INSTANCE;
};
}
Divertido? Agora podemos também aproveitar e dar o valor exato para quando temos um círculo:
static Valor perimetro(Object o) {
return switch (o) {
case Elipse(var b, var a) when a < b -> perimetro(new Elipse(a, b));
case Elipse(var a, var b) when a == b -> new Exato(2*Math.PI*a);
case Elipse(var a, var b) -> new Range(Math.sqrt(a*a + b*b) * 4, 4*a + 4*b)
.restringirMin(2*Math.PI*a)
.restringirMax(2*Math.PI*b);
case Diamante(var a, var b) -> new Exato(Math.sqrt(a*a + b*b) * 4);
case Retangulo(var a, var b) -> new Exato((a+b)*2);
default -> Invalido.INSTANCE;
};
}
System.out.println(perimetro(new Elipse(5, 5)));
// Exato[v=31.41592653589793]
System.out.println(perimetro(new Diamante(5, 5)));
// Exato[v=28.284271247461902]
System.out.println(perimetro(new Retangulo(10, 10)));
// Exato[v=40.0]
Bem, lembra do padrão quando estava mostrando mônadas? Eu não consegui reaproveitar o cálculo do perímetro do retângulo e do diamante nessa primeira implementação, mas podemos fazer algo melhor: um switch-case apontando para os casos conhecidos!
static Exato perimetro(Retangulo r) {
return new Exato((r.a+r.b)*2);
}
static Exato perimetro(Diamante r) {
return new Exato(Math.sqrt(r.a*r.a + r.b*r.b) * 4);
}
static Valor perimetro(Elipse e) {
return switch (e) {
case Elipse(var b, var a) when a < b -> perimetro(new Elipse(a, b));
case Elipse(var a, var b) when a == b -> new Exato(2*Math.PI*a);
case Elipse(var a, var b) ->
new Range(perimetro(new Diamante(a, b)).v(), perimetro(new Retangulo(2*a, 2*b)).v())
.restringirMin(2*Math.PI*a)
.restringirMax(2*Math.PI*b);
};
}
static Valor perimetro(Object o) {
return switch (o) {
case Elipse e -> perimetro(e);
case Diamante d -> perimetro(d);
case Retangulo r -> perimetro(r);
default -> Invalido.INSTANCE;
};
}
System.out.println(perimetro(new Elipse(5, 5)));
// Exato[v=31.41592653589793]
System.out.println(perimetro(new Diamante(5, 5)));
// Exato[v=28.284271247461902]
System.out.println(perimetro(new Retangulo(10, 10)));
// Exato[v=40.0]
Object o1 = new Elipse(4, 5);
System.out.println(perimetro(o1));
// Range[min=25.612496949731394, max=31.41592653589793]
Object o2 = new Elipse(5, 4);
System.out.println(perimetro(o2));
// Range[min=25.612496949731394, max=31.41592653589793]
Java moderno e a aritmética de Peano
Tudo isso foi só para apresentar as características interessantes que vou usar do Java moderno para fazer aritmético de Peano. Pattern-mathing, sealed interfaces, são ferramentar para aumentar a expressividade do Java.
Vou fazer baseado neste post: Aritmética de Peano em Haskell. Recapitulando a construção básica do que estamos lidando:
- existe o número natural 0
- todo número sucessor de um número natural é também um número natural
Pegando do artigo sobre Haskell, basicamente eu tenho os naturais como sendo o zero ou o sucessor de outro natural. Para expressar isso em Java:
sealed interface Nat {
record Zero() implements Nat {
static final Zero INSTANCE = new Zero();
}
record Suc(Nat prev) implements Nat {}
default Suc suc() {
return new Suc(this);
}
}
Soma
Como estamos com Java, podemos fazer algumas coisas que com o Haskell não era
tão natural. Por exemplo, posso aqui colocar a função de soma no tipo Zero,
e no tipo Suc fazer o pattern-matching:
public sealed interface Nat {
static Zero zero() {
return Zero.INSTANCE;
}
record Zero() implements Nat {
static final Zero INSTANCE = new Zero();
@Override
public Nat add(Nat b) {
return b;
}
}
record Suc(Nat n) implements Nat {
@Override
public Nat add(Nat b) {
return switch (b) {
case Zero z -> this;
case Suc(var bn) -> this.suc().add(bn);
};
}
}
Nat add(Nat b);
default Suc suc() {
return new Suc(this);
}
}
final var dois = zero().suc().suc();
System.out.println(dois);
// Suc[n=Suc[n=Zero[]]]
System.out.println(dois.add(dois));
// Suc[n=Suc[n=Suc[n=Suc[n=Zero[]]]]]
Isso foi um porte do pensamento direto do Haskell, não tenho muito a acrescentar aqui.
Valor numérico
Vou facilitar o meu debug: permitir obter um valor numérico a partir de um
Nat. A ideia é simples: zero tem zero, o sucessor de um natural é 1 mais o
valor numérico do número base. E para fazer uma chamada de cauda bonita, vamos
ter um método passando o acumulador:
public sealed interface Nat {
// ...
int numericValue();
default int numericValueTailCall() {
return numericValueTailCall(0);
}
int numericValueTailCall(int acc);
record Zero() implements Nat {
// ...
@Override
public int numericValue() {
return 0;
}
@Override
public int numericValueTailCall(int acc) {
return acc;
}
}
record Suc(Nat n) implements Nat {
// ...
@Override
public int numericValue() {
return 1 + n.numericValue();
}
@Override
public int numericValueTailCall(int acc) {
return n.numericValueTailCall(acc + 1);
}
}
}
final var dois = zero().suc().suc();
System.out.println(dois.numericValue());
// 2
System.out.println(dois.add(dois).numericValue());
// 4
System.out.println(dois.numericValueTailCall());
// 2
System.out.println(dois.add(dois).numericValueTailCall());
// 4
Pelo menos agora ficou mais fácil de depurar.
Multiplicar
De novo, bebendo do post que eu fiz sobre aritmética de Peano em Haskell, sem muito a acrescentar:
public sealed interface Nat {
// ...
Nat mult(Nat b);
record Zero() implements Nat {
// ...
@Override
public Nat mult(Nat b) {
return this;
}
}
record Suc(Nat b) implements Nat {
// ...
@Override
public Nat mult(Nat b) {
return switch (b) {
case Zero z -> z;
case Suc(var bn) -> this.add(this.mult(bn));
};
}
}
}
final var dois = zero().suc().suc();
final var tres = dois.suc();
System.out.println(dois.add(tres).numericValueTailCall());
// 5
System.out.println(dois.mult(tres).numericValueTailCall());
// 6
System.out.println(dois.add(tres).mult(tres).numericValueTailCall());
// 15
Menor que
Antes de seguir com o “módulo e divisão”, no post sobre Aritmética de Peano em Haskell eu segui por uma tangente antes: menor que.
Então, vamos lidar com isso aqui. Basicamente, preciso subtrair dois números
até chegar em algum deles ser zero. E como faremos isso com Java? Usando
obviamente um record apropriado e muito pattern-matching!
Basicamente agora vou ter um record Par(Nat a, Nat b) {} interno e vou fazer
ele casar com as seguintes opções:
Par(Zero a, Zero b)Par(Suc(Nat a), Zero b)Par(Zero a, Suc(Nat b))Par(Suc(Nat a), Suc(Nat b))
Sim, Java permite fazer deep-destructuring! Isso é divertido!
static boolean menorQue(Nat l, Nat r) {
record Par(Nat a, Nat b) {};
return switch (new Par(l, r)) {
case Par(Zero a, Zero b) -> false;
case Par(Zero a, Suc(Nat b)) -> true;
case Par(Suc(Nat a), Zero b) -> false;
case Par(Suc(Nat a), Suc(Nat b)) -> menorQue(a, b);
};
}
final var dois = zero().suc().suc();
final var tres = dois.suc();
System.out.println(menorQue(dois, tres));
// true
System.out.println(menorQue(dois, dois));
// false
System.out.println(menorQue(tres, dois));
// false
Se eu quiser mudar para maiorQue, menorIgual, só alterar as 3 constantes
que aparecem nos retornos. Cada combinação de true/false vai dar uma operação
distinta:
true,true,true-> tautologiatrue,true,false-> menor igualtrue,false,true-> maior igualfalse,true,true-> diferentetrue,false,false-> igualdadefalse,true,false-> menor quefalse,false,true-> maior quefalse,false,false-> contradição
Portanto, se eu quisesse usar a mesma estrutura para as outras operações, eu poderia fazer o seguinte:
- ponto de entrada
menorQue - chama a função de
reductioAdNullaque recebe 2 naturais e um vetor booleanos com 3 posições, passando aoreductioAdNullao vetorMENOR_QUE - deixa o
reductioAdNullacuidar da recursão - no caso não recursivo, retorna
respostas[0],respostas[1]ourespostas[3]se for o primeiro, segundo ou terceiro matching
boolean[] MENOR_QUE = { false, true, false };
static boolean menorQue(Nat l, Nat r) {
return reductioAdNulla(l, r, MENOR_QUE);
}
private static boolean reductioAdNulla(Nat l, Nat r, boolean[] respostas) {
record Par(Nat a, Nat b) {};
return switch (new Par(l, r)) {
case Par(Zero a, Zero b) -> respostas[0];
case Par(Zero a, Suc(Nat b)) -> respostas[1];
case Par(Suc(Nat a), Zero b) -> respostas[2];
case Par(Suc(Nat a), Suc(Nat b)) -> reductioAdNulla(a, b, respostas);
};
}
Mas eu poderia ser ainda mais fancy. Afinal, eu preciso de 3 booleanos, e
passar um array é uma maneira de se fazer isso. Sabe o que tem 32 booleanos
armazenados e é trivial de passar? Um inteiro. Então eu posso simplesmente
atribuir flags (tais quais 0, 1 e 2) para posições do vetor e usar isso. E
passar um único inteiro de flags. Vamos imaginar para o caso
Par(Zero a, Suc(Nat b)) inicialmente, que no vetor de booleanos retorno
respostas[1]. Nesse caso, vamos verificar se a flag 2 está ligada no número
e, estando diferente de zero, retorna true. Algo como:
case Par(Zero a, Suc(Nat b)) -> (flags & 2) != 0;
Mas como estamos em Java, constantes mágicas não são assim tão bem vindas. Não só em Java, mas tem outros lugares também. Então posso atribuir 3 flags:
EQ_FLAG = 1LT_FLAG = 2GT_FLAG = 4
E esse case ficaria:
case Par(Zero a, Suc(Nat b)) -> (flags & LT_FLAG) != 0;
E como seriam as funções de entrada, tipo maiorIgual? Basicamente passaria
para flags o valor EQ_FLAG | GT_FLAG. Aqui só exemplificando algumas dessas
comparações:
int EQ_FLAG = 1;
int LT_FLAG = 2;
int GT_FLAG = 4;
static boolean menorQue(Nat l, Nat r) {
return reductioAdNulla(l, r, LT_FLAG);
}
static boolean menorIgual(Nat l, Nat r) {
return reductioAdNulla(l, r, LT_FLAG | EQ_FLAG);
}
private static boolean reductioAdNulla(Nat l, Nat r, int flags) {
record Par(Nat a, Nat b) {};
return switch (new Par(l, r)) {
case Par(Zero a, Zero b) -> (flags & EQ_FLAG) != 0;
case Par(Zero a, Suc(Nat b)) -> (flags & LT_FLAG) != 0;
case Par(Suc(Nat a), Zero b) -> (flags & GT_FLAG) != 0;
case Par(Suc(Nat a), Suc(Nat b)) -> reductioAdNulla(a, b, flags);
};
}
Subtração
Sabe o reductioAdNulla? Ele está fazendo subtração, de certa forma. Então, se
por acaso eu seguir por esse rumo, usando as mesmas convenções feitas em
Aritmética de Peano em Haskell de
que se a < b ==> a - b = 0 para manter tudo nos naturais, posso retornar zero
ou o valor associado no caso não zero. Usando o diffNat improtado do meu
outro post:
static Nat diffNat(Nat l, Nat r) {
record Par(Nat a, Nat b) {};
return switch (new Par(l, r)) {
case Par(Zero a, Zero b) -> l; // o lado esquerdo é zero mesmo
case Par(Zero a, Suc(Nat b)) -> l; // o lado esquerdo é zero mesmo
case Par(Suc(Nat a), Zero b) -> l; // o lado esquerdo é o que sobrou da diferença
case Par(Suc(Nat a), Suc(Nat b)) -> diffNat(a, b);
};
}
final var dois = zero().suc().suc();
final var tres = dois.suc();
System.out.println(diffNat(dois, tres).numericValueTailCall());
// 0
System.out.println(diffNat(tres, tres).numericValueTailCall());
// 0
System.out.println(diffNat(tres, dois).numericValueTailCall());
// 1
System.out.println(diffNat(tres.mult(tres), dois).numericValueTailCall());
// 7
Beleza. Mas podemos simplificar um pouco isso, já que os dois primeiros ramos
pode ser traduzido como Par(Zero a, Nat b):
static Nat diffNat(Nat l, Nat r) {
record Par(Nat a, Nat b) {};
return switch (new Par(l, r)) {
case Par(Zero a, Nat b) -> l; // o lado esquerdo é zero mesmo
case Par(Suc(Nat a), Zero b) -> l; // o lado esquerdo é o que sobrou da diferença
case Par(Suc(Nat a), Suc(Nat b)) -> diffNat(a, b);
};
}
Divisão e módulo
No post, usei um record Haskell para calcular ambos ao mesmo tempo. Vou
manter o mesmo comportamento aqui: record DivMod(Nat div, Nat mod) {}.
Na divisão eu calculo o DivMod de a por b e seleciono o r.div(). No
módulo, semelhante mas retornando r.mod(). A estratégia é a mesma:
- no começo, o acumulador é 0
- se o divisor for maior que o dividendo, retorna o acumulado para
dive o dividendo para módulo - senão, subtrai o divisor do dividendo, soma um no acumulado, e segue com
divMod
Aqui o código:
record DivMod(Nat div, Nat mod) {}
static DivMod divMod(Nat a, Nat b) {
return divModRec(a, b, zero());
}
private static DivMod divModRec(Nat a, Nat b, Nat acc) {
if (menorQue(a, b)) {
return new DivMod(acc, a);
}
return divModRec(diffNat(a, b), b, acc.suc());
}
final var dois = zero().suc().suc();
final var tres = dois.suc();
final var dezoito = tres.mult(tres).mult(dois);
final var cinco = tres.add(dois);
System.out.println(divMod(dezoito, cinco).div().numericValueTailCall());
// 3
System.out.println(divMod(dezoito, cinco).mod().numericValueTailCall());
// 3
E as operações de div e mod são extraídas diretamente de divMod:
static Nat mod(Nat a, Nat b) {
return divMod(a, b).mod();
}
static DivMod divMod(Nat a, Nat b) {
return divModRec(a, b, zero());
}