O algoritmo de Dijkstra é um algoritmo clássico para se buscar o menor caminho entre dois pontos de um grafo. Muitas vezes ele é tratado como um tabu, como algo difícil. E eu estou aqui para tentar desmistificar isso e mostrar que ele pode ser tranquilo de entender.

Definindo o problema do menor caminho

Bem, pra falar de Dijkstra precisamos falar de grafos, e precisamos também definir o problema em questão. Então, que tal formular o que é um grafo?

vamos lá… um grafo são vários pontos conectados.

Pronto.

Só isso.

Isso é um grafo.

Bicho de sete cabeças? Não né?

Ok. Vamos em frente.

Dito isso, normalmente damos alguma espécie de “nome” a esses pontos. Nem que seja um simples número, pois assim podemos falar sobre o ponto em específico mais tarde.

As conexões de um grafo podem ter características. Uma das mais importantes é a “distância”, ou peso. Por exemplo, temos os pontos Fortaleza e Natal, e a distância entre eles é de 525.

Grafos podem ter muito mais nuances do que isso, mas o principal é isso. Temos pontos. Eles normalmente são nomeados, mas podem ter outras propriedades. Temos ligações entre os pontos. Essas ligações podem ter propriedades.

A nomenclatura que se dá para os pontos é “vértices”, e para as ligações/conexões entre esses pontos chamamos de “arestas”. Normalmente o grafo é representado como sendo uma tupla $\langle V, E \rangle$, onde $V$ é o conjunto de vértices e $E$ (vem de edge, que significa “aresta” em inglês) é o conjunto de arestas, na forma $\langle v_{out}, v_{in}, d\rangle$ onde $v_{out}$ é o vértice de origem, $v_{in}$ é o vértice de destino, $v_{out}, v_{in} \in V$ e $d$ é a distância dessa aresta.

Nem todo vértice se liga a todo vértice, mas mesmo assim podemos alcançar um vértice dando alguns saltos. Um vértice $a$ é dito vizinho do vértice $b$ se existir alguma aresta $\langle a, b\rangle \in E$; neste caso específico, eu consigo sair de $a$ e chegar em $b$ porque tem uma aresta ligando $a\rightarrow b$. Se por acaso eu consigo alcançar $c$ a partir de $b$ porque existe $b\rightarrow c$, então eu consigo alcançar $c$ a partir de $a$ também.

A partir de um vértice, eu consigo alcançar alguns outros vértices do grafo. Se eu tenho dentro do alcance de $a$ (chamemos de $A_a$) o vértice $c$, então isso significa que:

• $c = a$; ou
• existe um caminho de $a$ para $c$

Tá, mas o que é um caminho? Um caminho é uma lista de arestas. Mas essa lista satisfaz uma propriedade muito importante: o vértice de origem do próximo elemento da lista é o vértice de destino do elemento anterior (considerando que a lista é indexada a partir do 0):

$\forall i \in \left(0, \left|P\right|\right]: p_{i-1}.v_{in} = p_i.v_{out} \\ \forall p_i \in P \implies p_i \in E$

O caminho tem origem em $p_0.v_{out}$ e chega em $p_{último}.v_{in}$. Com isso, temos a pergunta: saindo do vértice $a$, qual a menor distância percorrida para se chegar no vértice $b$ (considerando que seja possível sair de $a$ e chegar em $b$)?

Buscas em grafos

Existem dois algoritmos clássicos para grafos:

• busca em largura
• busca em profundidade

Podemos usar ambos para saber qual o alcance de um determinado vértice.

Busca em profundidade:

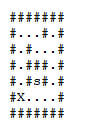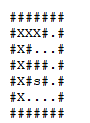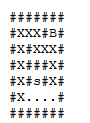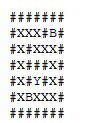
Busca em largura:

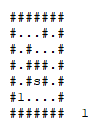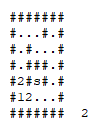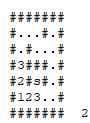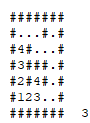
Usando essas buscas, é possível determinar o alcance que um vértice tem, assim como também é possível parar a busca quando se encontra que um vértice desejado é alcançável.

Ambos os algoritmos de busca seguem o mesmo esquema:

def busca(origem, destino):
    estrutura_dados = EstruturaDados()
    estrutura_dados.push(origem)
    jah_visitados = set()

    while not estrutura_dados.empty():
        sendo_visitado = estrutura_dados.pop()
        if sendo_visitado == destino:
            return True
        if not sendo_visitado in jah_visitados:
            jah_visitados.add(sendo_visitado)

            for v in sendo_visitado.vizinhos():
                if not v in jah_visitados:
                    estrutura_dados.push(v)
    return False

Para fazer a busca em largura, usamos uma fila. Para fazer a busca em profundidade, usamos uma pilha. Note que é comum usar a pilha na busca em profundidade de modo implícito, como uma função recursiva.

Agora, e se fizéssemos uma pequena alteração? No lugar de pegar seguindo os protocolos FIFO para a fila ou LIFO para a pilha, que tal usar um esquema de prioridade?

A menor distância

Ok, vamos por agora na estrutura de dados não apenas o vértice, mas também a distância percorrida até o vértice:

def busca(origem, destino):
    estrutura_dados = EstruturaDados()
    estrutura_dados.push((origem, 0))
    jah_visitados = set()

    while not estrutura_dados.empty():
        sendo_visitado, distancia = estrutura_dados.pop()
        if sendo_visitado == destino:
            return distancia
        if not sendo_visitado in jah_visitados:
            jah_visitados.add(sendo_visitado)

            for v,d in sendo_visitado.vizinhos():
                if not v in jah_visitados:
                    estrutura_dados.push((v, distancia + d))
    return None

Note que adicionei também em cada elemento de vizinhos a distância para se chegar no vértice vizinho a partir do elemento atual, e caso seja impossível chegar no destino se retorna None.

Aqui, ao se sacar da estrutura de dados o par vértice/distância, essa distância será necessariamente a menor distância para se chegar naquele vértice em particular.

Demonstração: ao sacar um vértice obtemos menor distância

Começamos na origem. A partir dela, inserimos todos os seus vizinhos. Desses vizinhos, obtemos o de menor distância para a origem, conforme esperado. Digamos que a distância percorrida até esse primeiro vizinho a ser sacado é $d_1$, todos os vértices inseridos a partir desse vizinho incorrerão a distância $d_1$ mais a distância específica da aresta, portanto será $d_1 + e$, com $e \ge 0$.

Assim, nenhum novo vértice sendo sacado poderá ter um caminho menor do que um caminho de distância pelo menos $d_1$. O próximo vértice sacado terá acompanhado uma distância $d_2 \ge d_1$. Assim, todo novo saque será necessariamente de um vértice que já foi previamente visitado ou da menor distância possível para esse vértice.

Vamos levantar uma hipótese? E se por acaso sacarmos um vértice não visitado que não é a distância mínima? Pois bem, no saque do par vértice/distância é garantido que essa seja a menor distância possível (vamos chamar essa distância do vértice sacado de $d_h$). Portanto, os outros vértices que tem na coleção tem distância $d \ge d_h$. Logo, para a hipótese ser verdadeira, deveria ser necessária a existência desse mesmo vértice na coleção com uma distância $d < d_h$, porém isso não é possível.

Ao levantar a hipótese de que o vértice apareceria de novo na coleção com um valor menor, chegamos a conclusão que não é possível. Existe uma outra possibilidade que permitira essa hipótese ser verdadeira: se por acaso fosse possível inserir o vértice com uma distância menor do que $d_h$. A inserção de novos vértices para a coleção é sempre feita a partir da base (no caso aqui, começamos com $d_h$) mais a distância da aresta dessa base para o viziho dela. Portanto, essa soma sempre dá no mínimo $d_h$. Logo, não é possível inserir algum vértice na coleção que tenha um caminho menor do que $d_h$.

Daí chegamos a conclusão que o levantamento dessa hipótese sempre resultado em absurdos. Portanto, a sentença “ao sacar um vértice obtemos menor distância” é verdadeira quando o vértice é ainda não visitado.

A estrutura de dados

Vamos analisar implementações distintas para a estrutura de dados para o algoritmo de Dijkstra?

A implementação ingênua

Uma primeira abordagem é a abordagem mais ingênua possível: adicionar o elemento no final da lista. Para buscar sempre o menor da lista, se faz necessário que se faça uma busca pelo elemento com menor distância.

No começo, temos uma lista que será povoada. Inserir? Coloca no final, acabou. Para detectar que tá vazia? Olhemos a lista interna, se o tamanho for 0 então está vazio. Agora, para sacar… Para isso, precisamos ser capazes de detectar de dois elementos qual tem a precedência. Portanto, precisa-se de uma espécie de comparador ao iniciar a estrutura.

class NaiveLista:
    def __init__(self, comparator):
        self.internal = []
        self.comparator = comparator
    
    def push(self, n):
        self.internal.append(n)
    
    def pop(self):
        if len(self.internal) == 0:
            return None
        m = 0
        minimum_value = self.internal[0]
        for i, v in enumerate(self.internal):
            if self.comparator(v, minimum_value):
                minimum_value = v
                m = i
        self.internal.pop(m)
        return minimum_value

    def empty(self):
        return len(self.internal) == 0

Aqui, a inserção é $O(1)$, porém a remoção é $O(n)$.

Insertionsort-like

Aqui, inserimos um elemento no final e colocamos ele no lugar, tal qual uma operação do “insertion sort”. O pop é simplesmente pegar um elemento do começo, a complexidade está na inserção:

class InsertLista:
    def __init__(self, comparator):
        self.internal = []
        self.comparator = comparator
    
    def push(self, n):
        i = len(self.internal)
        self.internal.append(n)
        while i > 0 and self.comparator(n, self.internal[i-1]):
            self.internal[i], self.internal[i-1] = self.internal[i-1], self.internal[i]
            i -= 1
    
    def pop(self):
        if len(self.internal) == 0:
            return None
        return self.internal.pop(0)

    def empty(self):
        return len(self.internal) == 0

A inserção é $O(n)$ e remoção é $O(1)$.

Essas soluções apresentadas tem incovenientes fortes: elas são lentas. Operações de ordem linear. Uma operação de ordem linear para cada aresta inserida. Mas existe uma opção melhor do que essas apresentadas: podemos fazer com que as operações de inserção/remoção sejam logarítmicas.

Heap binária

Uma heap (binária) é uma estrutura de dados que tem essas duas características:

• é uma árvore (binária)
• todo nó filho é menos prioritário do que seu nó pai (ou tão prioritário quanto)
• todos os níveis estão cheios, exceto potencialmente o último

Como é uma árvore cheia, sua altura é sempre cerca de $\lceil\log_2(n)\rceil$. Trabalhando com essas premissas, precisamos lidar com a inserção e com a remoção de elementos para garantir isso. Então, vamos lidar com a inserção primeiro?

Ao inserir o elemento, não sabemos em que lugar ele precisa estar no final das contas. Mas podemos colocar ele logo de cara no final da árvore e, a partir daí, ir promovendo ele. Então, coloquemos ele na primeira posição livre da árvore ou no nível seguinte. A partir desse momento, existem duas situações:

• o novo nó tem prioridade igual ou menor do que a do nó pai
• o novo nó tem prioridade maior do que a do nó pai

No primeiro caso, a heap se mantém bem ordenada, acabamos o processamento. Agora, no segundo caso, precisamos trocar de posição com o pai. Processo que eu chamo de promover o elemento, ou simplesmente promoção do elemento.

Ah, e se trocar a posição e ficar menos prioritário que o nó irmão?

Vamos examinar essa hipótese. Temos aqui o nó pai, que tem prioridade $p$, o nó anterior que tem prioridade $a$ e o nó novo que tem prioridade $n$. Como é uma heap e ela estava ordenada antes, sabemos que $p \ge a$. Como ao adicionar o nó novo deixamos a heap bagunçada, então $n > p$. Daí, como $p \ge a$ e $n > p$, chegamos a conclusão que

$n > p \ge a\\\therefore\\ n > a$

Caso resolvido para inserção. O elemento do topo necessariamente será o mais prioritário. Então, ao remover, vamos ter um valor vazio no topo, e portanto devemos rebalancear a heap. A estratégia que eu tenho em mente é trazer o último elemento para a primeira posição, e então a partir daí rebaixar ele até a posição adequada (processo de rebaixamento).

A operação de rebaixar um nó, tal qual a promoção do nó, precisa ser repetida toda vez que acontece um rebaixamento. Então, enquanto houver rebaixamento, faz de novo o processo para verificar se precisa rebaixar de novo na nova posição, até não ser possível rebaixar.

Nessa situação, temos que o nó pai é o nó problemático. Então vamos lidar com os nós $p$ para o nó pai, $e$ para o nó filho da esquerda e $d$ para o nó filho da direita. Existem algumas situações aqui:

• o nó não tem filhos
• o nó só tem o filho da esquerda
• o nó tem dois filhos

No caso de não ter mais filhos, não temos nenhum problema, a heap está bem ordeanda, tudo já está resolvido.

No caso de ter apenas o filho da esquerda, ainda temos 2 opções:

• $p \ge e$
• $p < e$

No primeiro desdobramento, a heap continua ordenada, não temos o que fazer. No segundo caso, precisamos trocar de posição os elementos $p$ e $e$.

Agora, para o caso interessante, em que existam os dois filhos. Nesse caso, não temos garantido aqui se $e > d$ ou se $d > e$. Se $p < e$ ou se $p < d$ vai ser necessário fazer um rebaixamento. E precisamos fazer o rebaixamento de modo que o heap continue ordenado! Portanto, se precisar haver rebaixamento, $p$ troca de lugar com o maior entre $e$ e $d$, pois assim o novo nó pai será maior do que ambos os filhos, mesmo que $p$ seja um valor intermediário entre $e$ e $d$.

De modo geral, é só isso. Porém… sabe como é, né? O diabo mora nos detalhes. Uma coisa legal é que para usar uma árvore não precisamos ter, literalmente, a árvore. Podemos simplesmente encodar a árvore em um array! Haha!

E como faríamos isso? Bem, precisamos de uma relação “única” entre o índice de um nó com seu pai, desse nó com o filho a esquerda e com o filho da direita. Independente de detalhes, as seguintes propriedades devem ser satisfeitas para encodar uma árvore binária em um array:

# para todo idx
idx_esq = idx_nodo_filho_esq(idx)
idx_dir = idx_nodo_filho_dir(idx)

idx_nodo_pai(idx_esq) == idx_nodo_pai(idx_dir) and idx == idx_nodo_pai(idx_esq)

Também precisa demonstrar também que a imagem da função idx_nodo_filho_esq é disjunta da imagem da função idx_nodo_filho_dir, e que ambas as funções são bijuntutivas.

Se o índice começasse em 1, poderia ser feito da seguinte maneira:

def idx_nodo_pai(idx_atual):
    return idx_atual//2

def idx_nodo_filho_esq(idx_atual):
    return 2*idx_atual

def idx_nodo_filho_dir(idx_atual):
    return 2*idx_atual + 1

Os filhos são únicos de cada pai, pois para um valor i qualquer, há apenas um valor de nodo pai que pode gerar ele. Se i for par, então ele é o filho a esquerda de alguém, e se i for ímpar, ele é o filho a direita de alguém. E ambos os filhos apontam para o mesmo pai, pois na divisão inteira o + 1 de 2*idx_atual + 1 não implica em diferença.

Mas… eu quero começar com o índice 0. Então, como lidar com isso? Bem, fiz da seguinte maneira:

def idx_nodo_pai(idx_atual):
    return (idx_atual-1)//2

def idx_nodo_filho_esq(idx_atual):
    return (idx_atual+1)*2 -1

def idx_nodo_filho_dir(idx_atual):
    return (idx_atual+1)*2

Não fiz prova rigorosa disso, mas funcionou adequadamente nos testes. Fica ao leitor demonstrar isso.

Bem, e como fica a implementação dessa estrutura de dados heap-like? Sem delongas, fica assim:

class HeapLike:
    def __init__(self, comparator):
        self.internal = []
        self.comparator = comparator
    
    def push(self, n):
        i = len(self.internal)
        self.internal.append(n)

        if i == 0:
            # caso trivial: lista vazia
            return
        nodo_pai = HeapLike.nodo_pai(i)
        while self.comparator(n, self.internal[HeapLike.nodo_pai(i)]):
            self.internal[i] = self.internal[nodo_pai]
            self.internal[nodo_pai] = n
            i = nodo_pai
            if i == 0:
                break
            nodo_pai = HeapLike.nodo_pai(i)

    @staticmethod
    def nodo_pai(n):
        return (n-1)//2
    
    @staticmethod
    def filho_esq(n):
        return (n+1)*2 -1
    
    @staticmethod
    def filho_dir(n):
        return (n+1)*2

    def pop(self):
        r = self.internal[0]
        tamanho = len(self.internal) - 1
        elemento_rebaixado = self.internal[tamanho]
        self.internal[0] = elemento_rebaixado
        self.internal.pop()

        i = 0
        while True:
            e = HeapLike.filho_esq(i)
            d = HeapLike.filho_dir(i)

            #print(f"tamanho {tamanho}, índices envolvidos {i} {e} {d}")
            if e >= tamanho:
                # chegou ao fim da heap
                break
            if d >= tamanho:
                # o nodo a esquerda ainda tá na heap, mas o da direita não
                # se precisar rebaixar, é apenas comparando com o da esquerda
                if not self.comparator(elemento_rebaixado, self.internal[e]):
                    # precisa trocar esquerda e índice atual
                    #print(f"trocando {self.internal[i]} idx {i} com {self.internal[e]} idx {e}")
                    self.internal[i], self.internal[e] = self.internal[e], self.internal[i]
                break
            if self.comparator(elemento_rebaixado, self.internal[e]) and self.comparator(elemento_rebaixado, self.internal[d]):
                # já está ordenado, não precisa de trocas
                break
            # agora, precisa detectar qual o índice alvo da troca
            target = e if self.comparator(self.internal[e], self.internal[d]) else d
            #print(f"envolvidos: {self.internal[i]} {self.internal[e]} {self.internal[d]}, índices {i} {e} {d}, trocando {self.internal[i]} idx {i} com {self.internal[target]} idx {target}")
            self.internal[i], self.internal[target] = self.internal[target], self.internal[i]
            i = target
        return r

    def empty(self):
        return len(self.internal) == 0

Sim, eu deixei os prints que usei para debugar de propósito.

Bem, tá aí. A parte mais complicada do algoritmo de Dijkstra, que nem é do algoritmo em si.

Note que aqui tanto a promoção quanto o rebaixamento são operações que ocorrem no máximo uma vez por nível da árvore. Como ao inserir um elemento rodamos sempre a promoção do elemento inserido, a inserção tem um tempo de $o(\log_2(n))$. A remoção de elemento nós pegamos o último elemento do array e colocamos na primeira posição e sempre fazemos o rebaixamento, portanto também roda em tempo $o(\log_2(n))$.

Um exemplo completo

Bem, vamos lá. Vou eventualmente precisar da estrutura de um grafo, vou fazer ela mais tarde. Mas antes vou identificar cada nó com um número sequencial, começando de 0 e indo até n-1, onde n é o total de vértices do grafo. A partir desse índice, posso perguntar para o grafo quais são os nós vizinhos, que retornarei uma lista de (idx_vizinho, dist), algo como vizinhanca = grafo.vizinhos(0). Dito isso, vamos fazer o algoritmo der Dijkstra?

Ele irá receber o grafo em questão, o nó de origem, e o nó de destino:

# g é o grafo em si, origem é o índice de origem e destino é o índice de destino
def busca_dijkstra(g, origem, destino):
    estrutura_dados = HeapLike(lambda a,b: a[1] <= b[1])
    estrutura_dados.push((origem, 0))
    jah_visitados = set()

    while not estrutura_dados.empty():
        sendo_visitado, distancia = estrutura_dados.pop()
        if sendo_visitado == destino:
            return distancia
        if not sendo_visitado in jah_visitados:
            jah_visitados.add(sendo_visitado)

            for v,d in g.vizinhos(sendo_visitado):
                if not v in jah_visitados:
                    estrutura_dados.push((v, distancia + d))
    return None

A HeapLike é a estrutura de dados definida previamente.

E, finalmente, o grafo. Existem inúmeras representações possíveis para grafos. Aqui, vou escolher uma representação de grafos esparso: dado um grafo com n vértices, posso adicionar arestas através do método grafo.adiciona_aresta(v_out, v_in, w). Nesse caso, adicionaria a seguinte aresta ao grafo:

$v_{out}\xrightarrow{w} v_{in}$

Para o caso de arestas simétricas no grafo (ie, arestas que ligam $a\leftrightarrow b$), grafo.adiciona_aresta_bi(a, b, w):

$a\xleftrightarrow{w} b$

A implementação dela internamente como sendo adicionando duas arestas $a\rightarrow b$ e $b\rightarrow a$ com o mesmo peso:

class Grafo:
    #...
    def adiciona_aresta_bi(self, a, b, w):
        self.adiciona_aresta(a, b, w)
        self.adiciona_aresta(b, a, w)

Então, usando como exemplo o grafo que o Galego usou:

grafo = Grafo(5)
grafo.adiciona_aresta_bi(0, 1, 2)
grafo.adiciona_aresta_bi(0, 2, 4)
grafo.adiciona_aresta_bi(1, 2, 1)
grafo.adiciona_aresta_bi(1, 3, 7)
grafo.adiciona_aresta_bi(2, 3, 2)
grafo.adiciona_aresta_bi(2, 4, 10)
grafo.adiciona_aresta_bi(3, 4, 2)

print(f"a menor distâncie entre 0 e 4 é de {busca_dijkstra(grafo, 0, 4)}")

Para o grafo:

class Grafo:
    def __init__(self, n):
        self.arestas = [[] for _ in range(n)]

    def adiciona_aresta_bi(self, a, b, w):
        self.adiciona_aresta(a, b, w)
        self.adiciona_aresta(b, a, w)
    
    def adiciona_aresta(self, v_out, v_in, w):
        self.arestas[v_out].append((v_in, w))

    def vizinhos(self, idx):
        return self.arestas[idx]

Conclusão

O algoritmo de Dijkstra é um dos muitos algoritmos de busca em grafos. Os algoritmos de busca normalmente seguem o seguinte preceito:

• começa o ponto inicial em uma estrutura de dados
• repita até encontrar o desejado (ou até a estrutura ficar vazia, o que ocorrer primeiro)
• remova o elemento do topo
• se esse elemento já foi visitado no passado recente, ignora*
• bota os vértices vizinhos desse elemento de volta na estrutura de dados

O segredo do algoritmo de Dijkstra perante os outros algoritmos está na estrutura de dados usadas para guardar elementos futuras a se visitar, e que além do vértice também precisa carrear a distância total até o momento. E essa estrutura de dados é algo, bem dizer, independente do algoritmo de Dijkstra, bastando que ela retorne o elemento com maior prioridade quando for removido o elemento do topo.

Para uma melhor eficiência do algoritmo de Dijkstra, fazer a estrutura de dados como uma heap é o padrão. E a heap não é absurdamente difícil de implementar, muito menos em um array contíguo.

Quase toda a complexidade do algoritmo de Dijkstra reside na estrutura de dados para controlar a prioridade de qual o próximo vértice a ser resgatado.

Se desejar olhar os fontes, você pode encontrá-los no repositório do blog, nesta pasta: /assets/dijkstra-algorithm//py/.