Lukeberry Pi chegou com o seguinte desafio de programação competitiva:

Dado uma lista com diversas strings, diga qual o maior prefixo comum a todas as strings dessa lista?

Bem, isso me pareceu um problema pronto para se atacar com reduce, típico da programação funcional…

Mas, antes de mais nada, você já parou pra pensar: qual o tempo mínimo de espera para somar uma lista com n números aleatórios?

Fazendo somas

Pegue uma lista com n números, completamente dissociados uns dos outros. Como você faz para somar tudo?

Bem, a resposta para isso é bem simples: comece com um acumulador no valor neutro e então, para cada elemento desse conjunto, opere esse elemento com o acumulador e substitua o valor do acumulador. Algo que poderia ser descrito assim:

(lista: number[]) : number => {
    let acc = 0;
    for (let x of lista) {
        acc += x;
    }
    return acc;
}

A operação feita por isso é algo próximo a isto:

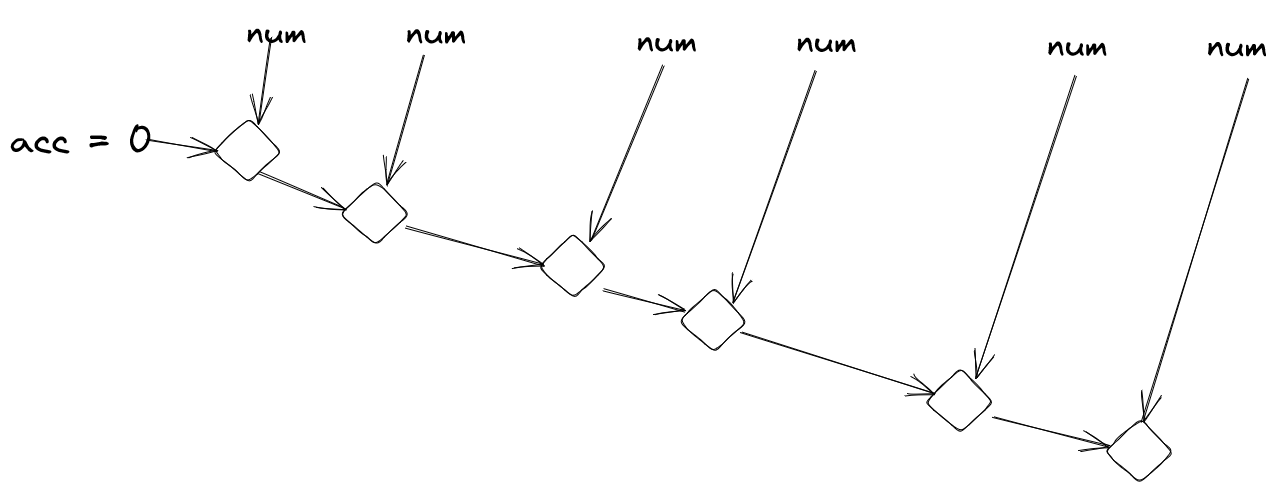
Árvore de operações de soma

Nota que aqui as operações são, basicamente:

  1. pegar elemento da lista e preparar para acumular
  2. acumular elemento preparado com acumulador
  3. repetir com novo acumulador

Mas, e se eu pudesse fazer esse mesmo processo com dois acumuladores distintos?

Por que falo isso? Ideia muito estranha? Bem, olhe a evolução temporal dessa soma que acabamos de realizar:

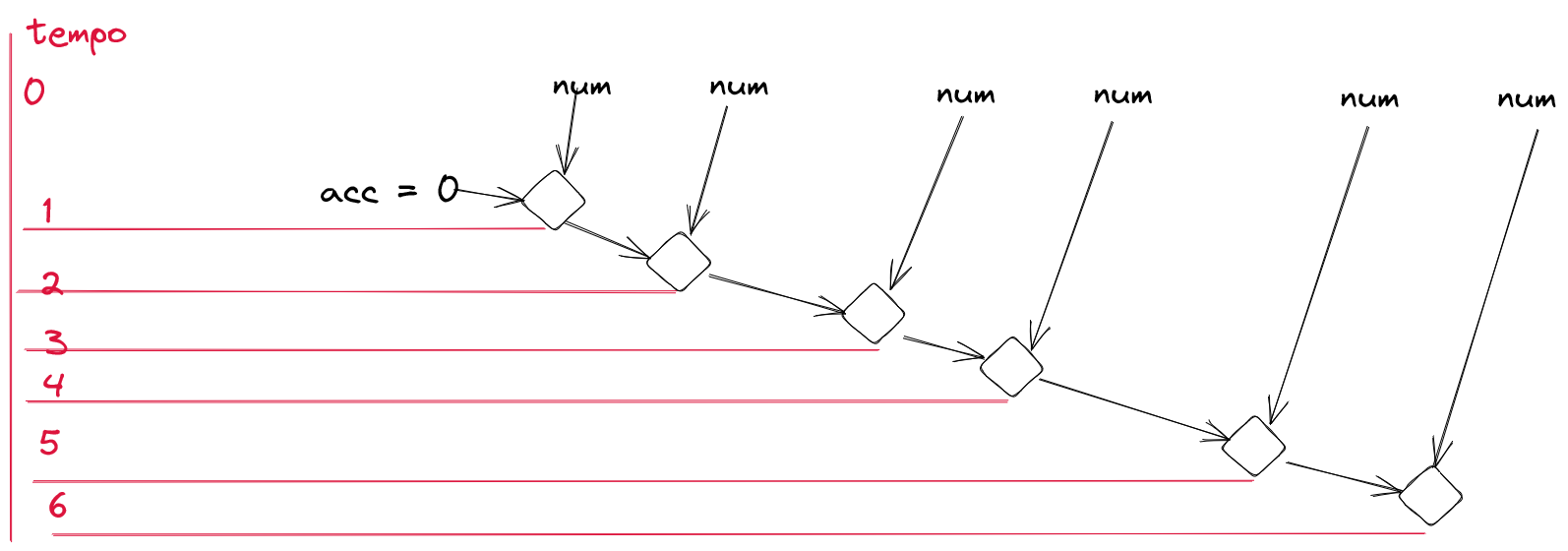
Árvore de operações de soma com eixo de tempo

Se eu puder juntar dois acumuladores, resultando em um novo acumulador, isso significa que a seguinte árvore de operações é possível:

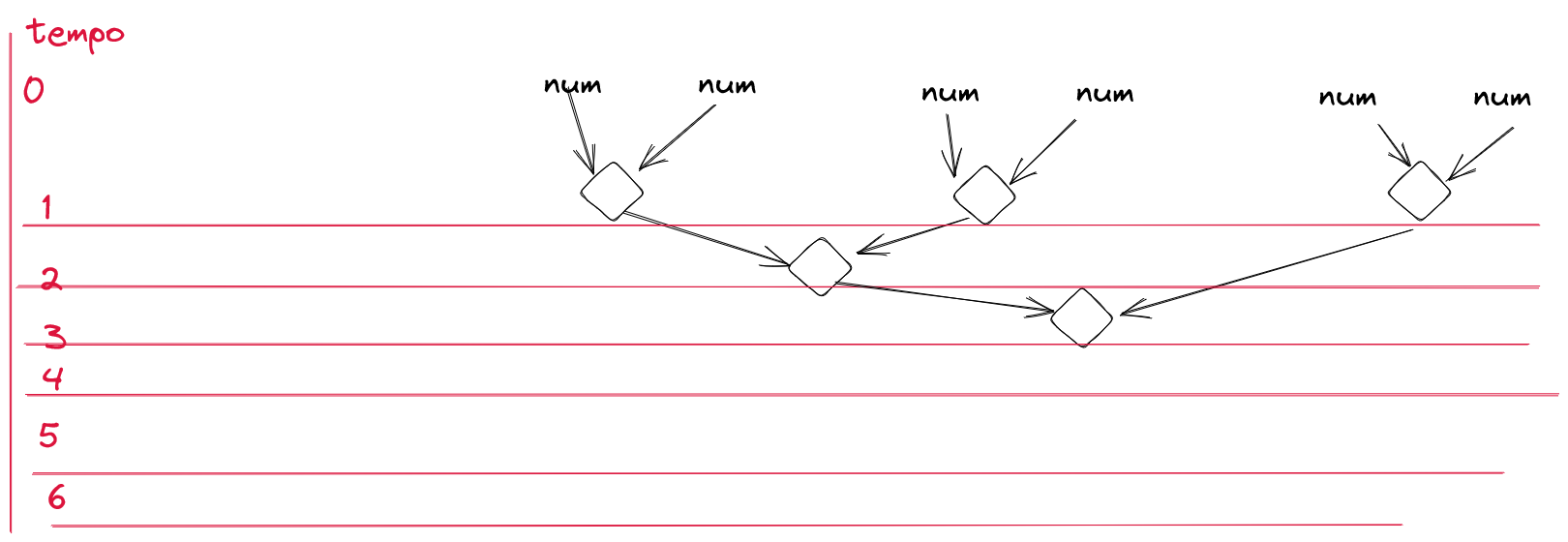
Árvore de operações de soma com eixo de tempo

O que antes se esperava por 6 operações, agora é esperado pelo tempo de 3 operações. Por mais que se realizem 5 operações, só precisa esperar por 3. Por quê? Bem, magia.

Antes que você, leitor, se pergunte “onde está a sexta operação que o Jeff deixou pra trás!?” saiba que, com o carinho adequado, ela poderia ter sido omitida da primeira árvore de soma, mas como eu já gerei a imagem e usei como base o elemento neutro, tem essa operação que surgiu a mais. Se, no lugar de ter usado o elemento neutro, eu tivesse pegue o primeiro elemento e acumulado a partir dele, então se teriam 5 operações.

Não qualquer magia, mas sim a magia do paralelismo. Como eu posso pegar acumuladores intermediários e eu sei operar em cima deles, então tanto faz a ordem com a qual faço as operações. Eu já posso operar os elementos 0 e 1 da lista ao mesmo tempo em que opera 2 e 3 e também simultaneamente 4 e 5.

Então, em cima desses 3 intermediários (0,1 e 2,3 e 4,5) eu preciso fazer a acumulação desses elementos, e agora para esse caso não é mais possível paralelizar. Mas, se tivesse mais um par, o 6,7, poderia acumular ele com 4,5 paralelo ao acúmulo de 0,1 com 2,3, resultando num tempo total de espera idêntico de 3 operações.

Então, se eu souber como juntar dois elementos acumulados, eu posso colocar paralelismo na questão e fazer as coisas serem mágicas. Eu posso sempre dividir a coleção de elementos em “acumular a metade da esquerda” e “acumular a metade da direita”, recursivamente até sobrar apenas dois elementos para juntar. Nesse momento, a “acumulação da esquerda” vai ser o elemento da esquerda preparado para acumulação, e a “acumulação da direita” vai ser o elemento da direita preparado para acumulação.

Nesse exemplo da soma, tem uma propriedade interessante: o elemento e o acumulador são do mesmo tipo. Então “preparar” o elemento para acumular é a função identidade Id: (n) -> n. E como o elemento da lista e o elemento acumulador são do mesmo tipo, saber como juntar um acumulador com um elemento da lista já me dá, imediatamente, como juntar um acumulador com outro acumulador.

Então, para fazer essa acumulação em paralelo, precisamos:

  1. pegar elemento da lista e preparar para acumular
  2. acumular elemento preparado com acumulador
  3. saber acumular dois acumuladores

Como o elemento da lista é o mesmo elemento da acumulação, então isso acaba se resumindo a uma única necessidade:

  1. acumular 2 elementos

Para os fãs de programação funcional, essa “acumulação” atende pelo nome de “redução”: vou reduzir uma lista a um único elemento, usando essa função redutora.

Comparando a soma via “tradicional” e via redução:

(lista: number[]) : number => {
    let acc = 0;
    for (let x of lista) {
        acc += x;
    }
    return acc;
}

(lista: number[]) : number => lista.reduce((acc, n) => acc + n)

O problema de máximo prefixo comum

Para encontrar o máximo prefixo comum, precisamos de duas strings as quais iremos operar, direta ou indiretamente. Sejam elas a e b. O resultado será uma possivelmente nova string c tal qual

c=a[0..max(i)]i  ⟹  ∀j<i,a[j]=b[j] c = a[0 .. max(i)] \\ i \implies \forall j\lt i, a[j] = b[j]

Essa definição já leva em consideração alguns pontos fortes:

  1. c necessariamente vai ser uma substring prefixo de a
  2. o comprimento de c nunca vai exceder o de a nem o de b
  3. possivelmente c pode ser vazio (com i = 0)
  4. c sempre será o maior possível prefixo encontrado entre esses dois

Agora, como encontrar essa string c de fato? Podemos receber as duas strings a e b e comparar caracter a caracter. No momento em que eu achar um caracter distinto, retorno o prefixo até (aberto) aquele caracter. Caso eu passe por tudo, pego o prefixo de a até o menor dos comprimentos das strings.

String prefixo2(String a, String b) {
    int minLen = Math.min(a.length(), b.length());
    for (int i = 0; i < minLen; i++) {
        // se distintos o caracter em i, já retorna
        if (a.charAt(i) != b.charAt(i)) {
            return a.substring(0, i);
        }
    }
    return a.substring(0, minLen);
}

Isso atende a necessidade para dois elementos. E para uma coleção?

Bem, aqui temos uma operação do tipo (X, X) => X. Podemos fazer isso continuamente para o caso de múltiplas entradas do mesmo tipo, basta que essa operação seja associativa.

Uma visão sobre redução

Tome uma coleção l de elementos L. Queremos reduzir essa coleção usando a operação op2: (L, L) => L.

Bem, temos duas opções para essa lista: ou ela é do tipo [hl | TL], com o elemento hl sendo o cabeçalho da lista e o resto da lista TL; ou ela é do tipo [], lista vazia.

Podemos definir então em cima de op2 uma função op_red: ([L]) => L|neutral, que recebe uma lista de elementos do tipo L e retorna um elemento do tipo L ou um elemento do tipo neutral, que pode até ser null sem problemas.

function op_red(lista: L[]): L|null { // aqui nulo marca o neutro
    if (lista.length == 0) {
        return null; // retorna o neutro
    }
    const hl = lista[0];
    const tl = lista.slice(1);
    const tl_red = op_red(tl); // redução do resto da lista
    if (tl_red == null) { // se for neutro, retorna o head
        return hl;
    }
    return op2(hl, tl_red);
}

Esse seria o jeito mais “clássico” de se pensar a redução, tal qual foi apresentado já nesta imagem:

Árvore de operações de soma com eixo de tempo

Mas se pegarmos de modo diferente a redução, podemos ter algo assim:

Árvore de operações de soma com eixo de tempo

Como alcançar isso? Bem, dividindo o problema em dois: metade da esquerda e metade da direita.

function op_red_half(lista: L[]): L|null { // aqui nulo marca o neutro
    const length = lista.length;
    if (length == 0) {
        return null; // retorna o neutro
    }
    const half = Math.floor(length/2);
    const left_list = lista.slice(0, half);
    const right_list = lista.slice(half);
    
    const left_red = op_red_half(left_list);
    const right_red = op_red_half(right_list);

    if (left_red == null) {
        // metade da esquerda gerou elemento neutro
        return right_red;
    }

    if (right_red == null) {
        // metade da esquerda tem valor e a da direita gerou neutro
        return left_red;
    }

    return op2(left_red, right_red);
}

Essa implementação em si não gera aquela árvore de operações acima descrita, pois separa exatamente no meio, portanto 3 elementos para cada lado. De toda sorte, a quantidade de operações totais e em paralelo e tempo de espera total se mantém.

Já ficou bem dividido agora, sempre resolvendo metade do problema por vez. Se o cálculo de left_red e de right_red forem feitos de maneira paralela, então teríamos que a execução desse algoritmo levaria tempo O(log n).

Reduzindo palavras para o prefixo

Em Java, já achamos o algoritmo que nos atende:

String prefixo2(String a, String b) {
    int minLen = Math.min(a.length(), b.length());
    for (int i = 0; i < minLen; i++) {
        // se distintos o caracter em i, já retorna
        if (a.charAt(i) != b.charAt(i)) {
            return a.substring(0, i);
        }
    }
    return a.substring(0, minLen);
}

Então, como recebemos um vetor de strings, podemos simplesmente pedir para que eles se comportem como uma stream de dados:

String[] palavras;
Stream.of(palavras).parallel().reduce(prefixo2);

E… pronto. O Java vai cuidar da mágica, já que a operação usada para reduce é garantida ser associativa e sem efeitos colaterais.

Agora, essa operação no Java, do jeito que está, retorna o neutro de um modo muito especial: Optional.empty(). E o valor também está incorporado a esse tipo Optional. Para pegar o valor guardado no Optional ou outra coisa a ser especificada, como por exemplo "" (string vazia), usamos o orElse:

String[] palavras;
Stream.of(palavras).parallel().reduce(prefixo2).orElse("");

Uma alternativa para evitar isso no Java é reduzir fornecendo um outro valor, mas que valor seria esse? Não existe valor bom o suficiente para representar todos os prefixos de string e ser válido em todos eles. Outro elemento “neutro” o suficiente seria o primeiro elemento da lista:

String[] palavras;
Stream.of(palavras).parallel().reduce(palavras[0], prefixo2);

Aqui estou usando a versão com valor neutro.

Mas essa alternativa é meio estranha… gera a cada redução uma string intermediária nova, mesmo que ela já seja o prefixo.

Envelopando a string e o tamanho

E se, no lugar de lidar diretamente com strings, trabalhássemos com algo que contemplasse uma string base e o tamanho do prefixo? Bem, por que não?

Posso inicialmente definir essa classe como sendo a Holder:

class Holder {
    final String prefix;
    final int len;

    Holder(String prefix) {
        this(prefix, prefix.length());
    }

    Holder(String prefix, int len) {
        this.prefix = prefix;
        this.len = len;
    }

    Holder acc(String another) {
        int prefixSize = prefixSize(another, another.length());
        if (prefixSize == len) {
            return this;
        }
        return new Holder(another, prefixSize);
    }

    Holder acc(Holder another) {
        int prefixSize = prefixSize(another.prefix, another.len);

        if (prefixSize == len) {
            return this;
        }
        if (prefixSize == another.len) {
            return another;
        }
        return new Holder(prefix, prefixSize);
    }
    
    private int prefixSize(String another, int anotherLen) {
        int x = anotherLen <= len? anotherLen: len;
        for (int i = 0; i < x; i++) {
            if (prefix.charAt(i) != another.charAt(i)) {
                return i;
            }
        }
        return x;
    }

    String prefix() {
        return prefix.substring(0, len);
    }
}

Note que essa classe gera o prefixo quando necessário: holder.prefix(). Note também que não é estritamente necessário guardar o prefixo em si, mas basta saber como chegar no prefixo.

Eu defini dois métodos de acumulação, porque estou visando usar a seguinte redução das streams: neutro, acumular com outra string, combinar com outro acumulador. Então, necessariamente é preciso colocar a acumulação com strings e, também, a combinação com outro Holder.

Bem, e isso funciona? Vamos analizar primeiro a função privada prefixSize. Essa função toma como argumentos duas strings e dois inteiros com os tamanhos respectivos das strings. Então, vai caminhando tentando detectar onde está o primeiro caracter distinto das duas strings. Não encontrando caracter distinto, retorna o menor tamanho de string.

Ah, mas Jeff, só tem dois argumentos, e você diz que ele trabalha com quatro, como que pode uma coisa dessas?

Simples, eu não estou levando mais em consideração o atributo oculto que existia originalmente, o this, e já estou trabalhando com ele “aberto”: a string e o tamanho que deve ser levado em consideração como prefixo.

Esse trecho em específico funciona. E no contexto onde ele está inserido?

Vamos lá, na acumulação com uma string nova. Se por acaso bater o tamanho do prefixo com o tamanho original, então posso simplesmente retornar this sem medo. Caso contrário é gerado um novo objeto com o valor correto para o tamanho do prefixo e uma string qualquer.

E, por fim, a combinação. A primeira pergunta que ele faz é se é do mesmo tamanho que ele. Se sim, se retorna. Caso contrário, verifica se é do tamanho do outro objeto sendo comparado. E no caso de não ser do tamanho de nenhum dos dois, é gerado um novo elemento.

Ok, até aqui parece feliz e tranquilo. Mas e o elemento neutro?

Pois bem, esse aí, para representar algum elemento que basicamente vai delegar para o outro o que se deve ser, acabei recorrendo a uma decisão difícil: criar um elemento para ser esse tipo de tarefa, usando de sobrecarga dos métodos.

Eu chamei esse cara de FIRST_HOLDER:

static final Holder FIRST_HOLDER = new Holder("", 0) {
    @Override
    Holder acc(String another) {
        return new Holder(another);
    }
    @Override
    Holder acc(Holder another) {
        return another;
    }
};

Ao receber uma acumulação, imediatamente tenho a criação do novo Holder. Na combinação, retorna logo de imadiatamente o valor do outro. E a existência dele implica em algumas pequenas alterações a serem feitas no método de combinação:

Holder acc(Holder another) {
    if (another == FIRST_HOLDER) {
        return this;
    }

    int prefixSize = prefixSize(another.prefix, another.len);

    if (prefixSize == len) {
        return this;
    }
    if (prefixSize == another.len) {
        return another;
    }
    return new Holder(prefix, prefixSize);
}

E como se usa isso? Bem, nesse exemplo estou recebendo as strings como um vetor clássico, mas fica aqui a ideia para outros usos:

private static String prefix(String[] args) {
    return Stream.of(args)
        .parallel()
        .reduce(FIRST_HOLDER, Holder::acc, Holder::acc)
        .prefix();
}

Usando coletores mutáveis

Resolvido o problema com reduce, mas ele gerou um efeito colateral que eu não gostaria de ter enfrentado: muita alocação de memória. As vezes só se desejava um outro valor para o tamanho do prefixo, mas não tinha essa opção…

Então, por que não usar a acumulação mutável do Java? O Java prevê, além do reduce, que é feito em cima de objetos imutáveis, o collect, que trabalha com um objeto de acumulação. Vamos então fazer a coleta desses valores?

Como é uma coleta, vamos estudar primeiro como se faz ela:

  1. preciso criar um objeto de acumulação
  2. preciso coletar, dentro de um objeto de acumulação, o objeto da stream
  3. mergear dois objetos de acumulação em um “terceiro”
  4. transformar o objeto de acumulação no resultado verdadeiro

Para mais informações, sempre vale a pena se referir ao javadoc da interface, Collector. Além dessa interface, tem o repositório de coletores utilitários descritos em Collectors. Essa lista fornece boa parte da soluções dos problemas que se encontra no dia-a-dia.

Sobre a coleta, ainda tem mais uma última coisinha: além dos métodos acima citados, ela também pode ter um conjunto de caraceterísticas. Esse conjunto de características fornecem uma dica pra JVM de como fazer a chamada de coleção.

Vamos lá, para as operações de acumulação e merge. Vou pegar como base o Holder usado no reduce e vou modificá-lo para que ele possa ser usado no collect, minimizando a necessidade de se alocar mais objetos. Vou chamar esse Holder mutável de… MHolder. Como se baseia em efeito colateral, não posso aqui me dar ao luxo de ter um FIRST_MHOLDER aos moldes do FIRST_HOLDER, então estou criando uma flag para indicar se está no estado inicial ou não (first):

public class MHolder {
    private final String prefix;
    private int len;
    private boolean first;

    private MHolder() {
        first = true;
        prefix = "";
        len = 0;
    }

    public MHolder(String prefix) {
        first = false;
        this.prefix = prefix;
        len = prefix.length();
    }

    public void acc(String another) {
        if (first) {
            this.prefix = another;
            len = another.length();
            first = false;
            return;
        }
        int prefixSize = prefixSize(another, another.length());
        this.len = prefixSize;
        return;
    }

    public MHolder acc(MHolder another) {
        if (first) {
            return another;
        }
        if (another.first) {
            return this;
        }
        int prefixSize = prefixSize(another.prefix, another.len);
        this.len = prefixSize;
        return this;
    }

    private int prefixSize(String another, int anotherLen) {
        int x = anotherLen <= len? anotherLen: len;
        for (int i = 0; i < x; i++) {
            if (prefix.charAt(i) != another.charAt(i)) {
                return i;
            }
        }
        return x;
    }

    public String prefix() {
        return prefix.substring(0, len);
    }

    public static MHolder first() {
        return new MHolder();
    }
}

E como seria o Collector derivado desse cara? Bem, seria assim (usando o factory method Collector.of):

Collector.of(
    // criação do container de valores intermediários
    MHolder::first,

    // acumular com objeto da lista
    MHolder::acc,

    // mergear ambos
    MHolder::acc,

    // deveria retornar um prefixo, né?
    MHolder::prefix
);

Muito bem, parece razoável. Vamos primeiro ver sobre a questão da criação do container (MHolder::first). Ele tem dentro de si o indicador que está no estado de fazer a primeira acumulação. Ao receber uma string, ele preenche o valor de seu prefix, o valor inicial de len e marca como já foi iniciado (first = false).

Operações de merge entre dois MHolders distintos, se um deles possuir a marca first como verdade, a resposta será o outro:

public MHolder acc(MHolder another) {
    if (first) {
        return another;
    }
    if (another.first) {
        return this;
    }
    // ...

E, no fluxo normal, como se comporta o objeto MHolder? Bem, o primeiro ponto é que, como se deseja o maior prefixo possível, vou usar uma única string no ciclo de vida inteiro da variável desse tipo. Só vou alterar o tamanho do prefixo.

Ao se coletar com outra string, passo pelo cálculo do maior prefixo conhecido e, então, atualizo o valor do tamanho do prefixo.

No caso do merge com outro acumulador, primeiro se certifica que o parâmetro não é o elemento neutro e, se for, retorna this. Caso contrário, faz o cálculo do prefixo baseado nos prefixos próprio e do parâmetro e nos tamanhos de prefixo próprio e do parâmetro.

Só isso? Bem, na verdade… não. Existe um último elemento que não tocamos ainda no assunto… ele é o varargs no final do método Collector.Characteristics... characteristics. Mas, o que são essas características do coletor?

Vamos lá, essa enum surgiu na versão 8 do Java e continua, até agora na versão 19, com os mesmos 3 possíveis valores:

  • CONCURRENT
  • IDENTITY_FINISH
  • UNORDERED

O que isso quer dizer? Bem, eles são dicas de otimização para que o executor dos pipelines das streams possam tomar uma decisão mais acertada do como lidar com as streams.

A propriedade IDENTITY_FINISH deve ser usada apenas quando o coletor for do tipo Collector<T, R, R>. Iremos retornar novamente a essas características após uma breve sidequest…

Sobre a tipagem dos coletores

Para quem vai consumir um coletor, a API que importa é apenas esta:

Collector<T, ?, R>

O segundo parâmetro é um detalhe interno de implementação, normalmente não tem impacto no lado externo. Mas, que parâmetros seriam esses, hein?

O primeiro parâmetro é o tipo de objeto que será reduzido. Isso significa que um coletor <String, ?, QqrCoisa> pode ser aplicado apenas para Stream<String>, não podendo ser aplicado para Stream<Abc> nem Stream<QqrCoisa>.

O terceiro parâmetro é o retorno que será produzido após a execução do coletor. Um coletor <String, ?, QqrCoisa> irá retornar algo compatível com QqrCoisa.

E finalmente tem o parâmetro do meio…

Esse parâmetro é importante para quem vai implementar o coletor, não para quem vai consumir o coletor. Vamos dar uma olhadinha nos métodos do coletor para tentar entender esse parâmetro do meio?

public interface Collector<T, A, R> {
    Supplier<A> supplier();
    BiConsumer<A,T> accumulator();
    BinaryOperator<A> combiner();
    Function<A,R> finisher();
    Set<Collector.Characteristics> characteristics();
}

O último método não importa, por agora, para falar sobre a tipagem dos genéricos do coletor. Ele será retornado mais tarde.

A primeira coisa que me chama atenção é um função A -> R, chamada de finalizadora, finisher. Basicamente, essa função está dizendo que é capaz de pegar algo em A e transformar em algo de R. Esse é o único método que faz algo com R.

Uma outra coisa que chama a atenção é o accumulator. Ele pega um elemento de A e um elemento de T e pronto. Some com eles. Esse é o único método que faz algo com T.

E então temos mais duas coisas curiosas:

  • Supplier<A> supplier: se consegue gerar um novo elemento de A
  • BinaryOperator<A> combiner: conseguimos pegar dois elementos de A e transformar em outro elemento de A

E como que funciona o coletor? Ainda não foi falado nada sobre esse A, apenas algumas evidências de coisas curiosas…

Bem, lembra quando se falava de redução no começo do artigo?

  1. pegar elemento da lista e preparar para acumular
  2. acumular elemento preparado com acumulador
  3. saber acumular dois acumuladores

Pois bem, deve ter notado que de modo pervasivo se usou a terminologia acumular. O A aqui é justamente o elemento de acumulação.

No coletor do Java, toda operação de acumulação é voltada a efeito colateral. Por isso que temos BiConsumer<A, T>, isso permite fazer algo como Set::add para juntar elementos do tipo T em um Set<T>, onde Set<T> seria o A do coletor em questão.

E o que seria o BinaryOperator<A> combiner? Bem, esse aí é um jeito de se pegar dois acumuladores distintos e fazê-los se misturarem. Note que aqui não se obriga a usar efeito colateral, pode-se retornar uma nova instância de acumulador. Isso permite fazer coisas desse tipo:

Árvore de operações de soma com eixo de tempo

Em que se pega dois acumuladores distintos e com o resultado dessa combinação continuar acumulando novos elementos ou se combinando com novos acumuladores.

Agora, e onde entra o Supplier<A> supplier nessa? Lembra do segundo passo? “acumular elemento preparado com acumulador”? Então, para acumular o acumulador deve primeiramente existir. Logo, precisamos de um acumulador. Neutro. E ele pode ser obtido chamando o resultado de Supplier<A>.

Como é uma função, posso gerar vários acumuladores neutros sem problema algum, e sair utilizando seus resultados para popular os elementos a serem acumulados em paralelo.

E o que seria o Function<A, T> finisher? Bem, ele vai basicamente terminar o serviço. Por exemplo, se eu quisesse um coletor de contagem de elementos únicos. A assinatura dele poderia ser Collector<T, ?, Integer>. Mas e o detalhe de implemetação? Então, vamos ver?

public Contador<T> implements Collector<T, Set<T>, Integer> {
    public Supplier<Set<T>> supplier() {
        return HashSet::new; // aqui usando HashSet só porque posso instanciá-lo
    }

    public BiConsumer<Set<T>,T> accumulator() {
        return Set::add;
    }

    public BinaryOperator<Set<T>> combiner() {
        return (antigo, novo) -> {
            antigo.addAll(novo);
            return antigo;
        };
    }

    public Function<Set<T>,Integer> finisher() {
        return Set::size;
    }

    public Set<Collector.Characteristics> characteristics() {
        return Collections.emptySet();
    }
}

Esse é o código que vai acumular e contar elementos distintos. E normalmente não se cria coletores assim (normalmente). O padrão para criação dos coletores é feita assim:

Collector.of(HashSet::new, Set::add, (antigo, novo) -> {
        antigo.addAll(novo);
        return antigo;
    }, Set::size);

Notou como o Set::size transforma de Set<T> -> Integer? Cumprindo portanto a promessa do coletor criado que é contar quantos elementos distintos há na stream?

Então, só para finalizar sobre a tipagem dos coletores:

  • T: o tipo do elemento de entrada
  • A: o elemento acumulador, normalmente detalhe de implementação
  • R: o resultado obtido

As características de coleta

Prometi que ia voltar, não prometi? Pois bem.

Recapitulando, no Java foram previstas três capacidades distintas para um coletor:

  • CONCURRENT
  • IDENTITY_FINISH
  • UNORDERED

E cada uma dessas permite uma otimização distinta.

IDENTITY_FINISH

Já foi citado aqui que o IDENTITY_FINISH só pode ser usado em coletores do tipo <T, R, R>. Como o tipo de acumulação é o mesmo do de retorno, é plausível esperar que a obtenção do resultado seja simplesmente o mesmo objeto de acumulação após acumular todos os elementos. Essa é a função identidade (representada por x -> x, também tem o Function.identity()).

Essa característica vai indicar para o processador de pipeline de map/reduce qual caminho a ser tomado. Aqui em específico indica que terminou de acumular, retorna, não precisa de mais um passo.

UNORDERED

Bem, esse cara aqui indica uma coisa importante para o executor da pipeline:

Pode executar em qualquer ordem aí que eu não me importo, manda que eu tanko!

Mas, como isso pode ser útil? Lembra que foi mencionado acima que para fazer reduções basta que a operação de redução seja associativa? Se além de ser associativa, ela for comutativa, então estamos numa situação em que não importa a ordem com a qual os elementos vem, estamos bem.

Exemplos de operações comutativas, que poderiam ser aplicadas para a coleta UNORDERED:

  • adicionar elementos em um Set*
  • somar inteiros
  • multiplicar inteiros

Aqui, não importa a ordem em que os elementos vem para se acumular, o resultado final é sempre equivalente.

Observação sobre adição de campos em um Set. O resultado final trará as mesmas respostas para as mesmas perguntas feitas a ele. Porém, como não tem garantia da ordem de inserção, talvez a performance seja bem distinta ao se fazer uma consulta. Por exemplo, tome um Set específico, vou chamar de ListSet. Ele trabalha inserindo os elementos no começo de uma lista ligada, removendo os nós da lista, e verificando todos os elementos da lista sequencialmente para saber se determinado elemento se encontra lá. Então, inserir os elementos 6, 2, 3 vai necessitrar de um tempo distinto para provar que o 6 está lá do que se for inserido 3, 2, 6.

Exemplos de operações que são extremamente dependentes da ordem de inserção e portato não deveriam ser usadas levianamente com UNORDERED:

  • join de strings
  • soma de floats
  • juntar em uma lista

Join de strings é fácil perceber. Pegue a string "A" e a string "B". Fazendo em uma ordem fica "AB" e em outra fica "BA". Portanto, não é comutativa.

Sobre juntar listas, é a mesma coisa da string. Listas por definição é uma estrutura de dados sensível à ordem. Portanto, A e B ao serem juntados em uma lista ficaria [A, B], porém ao inverter a ordem ficaria [B, A]. Essa operação não é comutativa.

Agora, sobre ponto flutuante… Bem, o problema com ponto flutuante é que ele é sensível às aglutinações. Suas operações são comutativas (ie, A+B == B+A para quaisquer A e B pontos flutuante), mas na real elas não são associativas. Basicamente, pontos flutuante de grandezas distinas (por exemplo, com expoente +3 e outro com +2) vão ter elementos da grandeza menor que são ignorados da grandeza maior. Vamos chamar esse diferencial ignorado de e.

Então, em ponto flutuante, assumindo que A > B, fazer A + B é equivalente a fazer A + B - e em números reais. Porém, se e é exatamente o trecho de B que é tão pequeno que é menosprezado na soma A + B, o que acontece se eu operar sucessivas vezes com ele?

(((A+B−e)−e)−e)−e (((A + B - e) - e) - e) - e

Com isso, como A+B−e==A+BA + B - e == A + B, podemos simplificar a operação de dentro para A + B, com isso restando apenas (((A+B)−e)−e)−e(((A + B) - e) - e) - e. Aplicando essa substituição mais três vezes, obtemos A+BA + B.

Mas, e se fizéssemos em outra ordem?

A+B+(((−e−e)−e)−e) A + B + (((- e - e) - e) - e)

Com isso, obtemos que −e−e-e -e é o dobro do que seria ignorado, mas como ee é exatamente o valor que seria irrelevante, multiplicar por 2 tornaria esse valor já minimamente relevante, de modo que isso já afetaria o resultado da conta. Multiplicando por 4 então…

E toda essa volta só para falar que somar pontos flutuante é extremamente sensível à ordem em que as operações são feitas.

Em que situações esse UNORDERED pode ser útil? Bem, se tivermos várias threads fazendo processamentos individuais, posso simplesmente acumular seus resultados independentemente de quando terminou, da ordem de invocação, essas coisas. Além disso, operações intermediárias que apenas servem para mudar a ordenação dos elementos (como .sorted()) podem ser ignoradas de maneira segura.

Poder fazer UNORDERED faz com que a árvore de merge de acumuladores possa seguir uma ordem 100% aleatória em maiores impactos. Como se quaisquer 2 pontos de resultados concluídos pudessem ser mesclados em ordem arbitrária:

Árvore de operações de soma com eixo de tempo

CONCURRENT

Essa característica indica que o coletor pode coletar em paralelo dois elementos distintos sem nenhum problema.

Lenda conta sobre o fato de que essa característica, se usada junto do UNORDERED, dá superpoderes aos coletores.

As propriedade do coletor de maior prefixo

Bem, vamos recuperar aqui a ideia do coletor do maior prefixo:

Collector.of(
    // criação do container de valores intermediários
    MHolder::first,

    // acumular com objeto da lista
    MHolder::acc,

    // mergear ambos
    MHolder::acc,

    // deveria retornar um prefixo, né?
    MHolder::prefix
);

Quais as características que ele precisa ter? Vamos examinar cada uma?

Pois bem, a primeira é IDENTITY_FINISH. Por que primeira? Porque essa é mais fácil verificar. Esse coletor termina com uma função identidade? Não? Pois bem, de fato eu saio de um coletor intermediário de prefixos para um elemento final.

Outro a se validar é UNORDERED. Precisa respeitar a ordem para que a coleta de prefixos seja bem realizada? Na real, também não, qualquer ordem tá boa.

E finalmente CONCURRENT. Infelizmente não sei o melhor jeito de trabalhar com ele, mas o código que escrevi está sujeito a dar ruim com acessos paralelos. Então, não, não pode ser CONCURRENT, não na incarnação atual dele.

Portanto, informando às características, o que teríamos como o coletor?

Collector.of(
    // criação do container de valores intermediários
    MHolder::first,

    // acumular com objeto da lista
    MHolder::acc,

    // mergear ambos
    MHolder::acc,

    // deveria retornar um prefixo, né?
    MHolder::prefix,

    // pode receber em qualquer ordem que tanka
    Collector.Characteristics.UNORDERED
);

Fechando tudo

A operação de achar o menor prefixo entre um conjunto de palavras é uma extrapolação de achar o menor prefixo entre duas palavras.

Um conjunto de elementos do tipo L pode ser reduzido para um único elemento do tipo L se existe uma função (L, L) -> L. É possível fazer uma redução ligeiramente diferente se for fornecido um elemento an do tipo A que seja “neutro” e uma operação (A, L) -> A.

Se a operação (L, L) -> L for associativa, então a redução poderá ser feita em paralelo, gastando tempo O(log n) considerando infinitos processadores e gratuidade na hora de sincronizar o processamento:

Árvore de operações de soma

Árvore de operações de soma com eixo de tempo

Podemos fazer uma redução em streams do Java usando a seguinte função:

String prefixo2(String a, String b) {
    int minLen = Math.min(a.length(), b.length());
    for (int i = 0; i < minLen; i++) {
        // se distintos o caracter em i, já retorna
        if (a.charAt(i) != b.charAt(i)) {
            return a.substring(0, i);
        }
    }
    return a.substring(0, minLen);
}

Como ela trabalha apenas com Strings, e Strings no Java são imutáveis, essa função não oferecerá mutabilidade para o redutor, portanto pode ser usada para redução com tranquilidade. O ponto negativo é que ela sempre gerará um novo elemento de memória. A chamada dela poderia ser assim:

String[] palavras;
Stream.of(palavras).parallel().reduce(prefixo2).orElse("");

Outra alternativa para evitar ficar gerando novos e novos elementos sempre seria na redução seria ter uma representação intermediária de acumulação, aqui representada pela classe Holder, cujo elemento neutro é Holder.FIRST_HOLDER:

class Holder {
    final String prefix;
    final int len;

    static final Holder FIRST_HOLDER = new Holder("", 0) {
        @Override
        Holder acc(String another) {
            return new Holder(another);
        }
        @Override
        Holder acc(Holder another) {
            return another;
        }
    };


    Holder(String prefix) {
        this(prefix, prefix.length());
    }

    Holder(String prefix, int len) {
        this.prefix = prefix;
        this.len = len;
    }

    Holder acc(String another) {
        int prefixSize = prefixSize(another, another.length());
        if (prefixSize == len) {
            return this;
        }
        return new Holder(another, prefixSize);
    }

    Holder acc(Holder another) {
        if (another == FIRST_HOLDER) {
            return this;
        }

        int prefixSize = prefixSize(another.prefix, another.len);

        if (prefixSize == len) {
            return this;
        }
        if (prefixSize == another.len) {
            return another;
        }
        return new Holder(prefix, prefixSize);
    }
    
    private int prefixSize(String another, int anotherLen) {
        int x = anotherLen <= len? anotherLen: len;
        for (int i = 0; i < x; i++) {
            if (prefix.charAt(i) != another.charAt(i)) {
                return i;
            }
        }
        return x;
    }

    String prefix() {
        return prefix.substring(0, len);
    }
}

E a chamada para a redução poderia ser assim:

String[] palavras;
Stream.of(palavras)
        .parallel()
        .reduce(FIRST_HOLDER, Holder::acc, Holder::acc)
        .prefix();

O Java também fornece a opção de fazer uma redução com um acumulador mutável. Esse acumulador pode ou não ser o estado final, tem casos em que vale a pena que o acumulador seja o retorno desejado, tem casos que não.

Baseado na ideia do Holder, podemos ter uma versão mutável MHolder que, no lugar de as vezes gerar uma nova variável, sempre irá manter uma variável:

public class MHolder {
    private final String prefix;
    private int len;
    private boolean first;

    private MHolder() {
        first = true;
        prefix = "";
        len = 0;
    }

    public MHolder(String prefix) {
        first = false;
        this.prefix = prefix;
        len = prefix.length();
    }

    public void acc(String another) {
        if (first) {
            this.prefix = another;
            len = another.length();
            first = false;
            return;
        }
        int prefixSize = prefixSize(another, another.length());
        this.len = prefixSize;
        return;
    }

    public MHolder acc(MHolder another) {
        if (first) {
            return another;
        }
        if (another.first) {
            return this;
        }
        int prefixSize = prefixSize(another.prefix, another.len);
        this.len = prefixSize;
        return this;
    }

    private int prefixSize(String another, int anotherLen) {
        int x = anotherLen <= len? anotherLen: len;
        for (int i = 0; i < x; i++) {
            if (prefix.charAt(i) != another.charAt(i)) {
                return i;
            }
        }
        return x;
    }

    public String prefix() {
        return prefix.substring(0, len);
    }

    public static MHolder first() {
        return new MHolder();
    }
}

Essa operação de acumulação, como e comutativa, posso adicionar ao Collector dela a característica UNORDERED. A chamada para a redução mutável poderia ser assim:

Collector<String, ?, String> coletorMaiorPrefixo = Collector.of(
    // criação do container de valores intermediários
    MHolder::first,

    // acumular com objeto da lista
    MHolder::acc,

    // mergear ambos
    MHolder::acc,

    // deveria retornar um prefixo, né?
    MHolder::prefix,

    // pode receber em qualquer ordem que tanka
    Collector.Characteristics.UNORDERED
);

// ...

String[] palavras;
Stream.of(palavras)
        .parallel()
        .collect(coletorMaiorPrefixo);

Complexidade dessas soluções

Considere que LL seja a lista de palavras, m=max(l),l∈Lm = max(l), l \in L e que n=size(L)n = size(L).

Serão realizadas sempre Θ(n)\Theta(n) operações. A opção com .reduce gerará novas alocações. Se usado prefix2: (String, String) -> String, serão gerados Θ(n)\Theta(n) elementos. Se usado a classe Holder, serão gerados O(n)O(n) elementos. Ambas as soluções tem a possibilidade de paralelizar as Θ(n)\Theta(n) operações, para um tempo de espera de O(log⁡2(n))O(\log_2(n)) operações. Cada operação roda em O(m)O(m).

Resumo da opção com .reduce:

  • complexidade temporal single thread: Θ(m×n)\Theta(m \times n)
  • complexidade temporal paralelismo gratuito infinito: O(m×log⁡2(n))O(m \times \log_2(n))
  • quantidade de memória alocada: Θ(n)\Theta(n) ou O(n)O(n)

Já a opção com .collect vai depender a quantidade de alocações. Se tiver em paralelo, serão alocados O(n)O(n) elementos, diretamente limitado pela quantidade de núcleos para fazer o processamento dessa redução mutável, enquanto que se for single thread será realizada uma quantidade finita de alocações (criação do acumulador, finalizador, e só), O(1)O(1). A análise de complexidade temporal se mantém a mesma de usando o .reduce:

Resumo da opção com .collect:

  • complexidade temporal single thread: Θ(m×n)\Theta(m \times n)
  • complexidade temporal paralelismo gratuito infinito: O(m×log⁡2(n))O(m \times \log_2(n))
  • quantidade de memória alocada: Θ(n)\Theta(n) se single thread, O(n)O(n) se paralelismo gratuito infinito

A solução do Lukeberry

Lukeerry deu uma solução bem engenhosa:

  • ordena a lista de palavras por ordem léxica
  • pegar o prefixo comum da primeira com a última palavra

Como se está usando a ordenação léxica, palavras com prefixo comum são agrupadas. Ao mudar algo no prefixo no n-ésimo caracter, a palavra com essa mudança estará necessariamente após todas as palavras que contém o prefixo até o n+1-caracter.

Como se tem uma ordenação, serão feitas O(nlog⁡n)O(n \log n) comparações de string, cada operação custando O(m)O(m) para ser calculada. A seguir, é realizada uma única operação de detecção de prefixo, num custo de també O(m)O(m). Nenhuma alocação fora as necessárias para a ordenação serão realizadas.

Ao todo, a complexidade temporal é de O(n×mlog⁡n)O(n\times m \log n).

Uma possível implementação em Java:

String[] palavras;
// ...
final int len = palavras.length;
if (len == 0) {
    return "";
}
if (len == 1) {
    return palavras[0];
}

Arrays.sort(palavras);
return prefixo2(palavras[0], palavras[len - 1]);