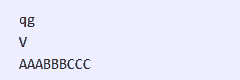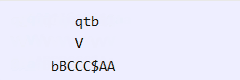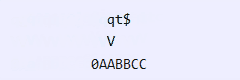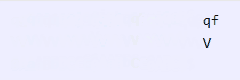O objetivo aqui é fazer um Autômato de Fila que consiga emular o funcionamento de uma
Máquina de Turing. Assumindo o teorema de que Máquinas de Turing são capazes de realizar
qualquer computação, a tarefa estaria completa. Porém, a primeira demonstração aqui será
mostrando que existe um algoritmo que transforma um Autômato de Fila em uma Máquina de Turing.
Essa demonstração será feita em duas partes. Nesta primeira parte, iremos simular um autômato de fila
através de uma máquina de Turing. Na segunda parte, iremos simular uma máquina de Turing através
de um autômato de fila;
Antes de podermos prosseguir, precisamos antes estabelecer algumas definições do que é cada
um desses autômatos, funções de transição e aceitação de entradas. Assim, daremos o fundamento
necessário para as duas partes desta demonstração.
Definições
Transições
Uma transição é uma função que mapeia um estado em outro, recebendo outros argumentos
eventualmente também.
Essa função pode ter dois ou mais mapeamentos distintos para a mesma entrada. Isso nos dá
o seguinte, para o exemplo de uma Máquina de Turing:
(Q,Σ)↦(Q,Σ,{⇐,⇒})
Pode gerar dois mapeamentos:
(q0,σ0)↦(q1,σ1,⇐)(q0,σ0)↦(q2,σ2,⇒)q0,q1,q2∈Q,σ0,σ1,σ2∈Σ
E isso estaria certo. Podemos dizer então que a função de transição é um elemento
dentro do conjunto δ que seja do seguinte formato:
t0∈δ⟹t0=(A,S⊂B+)
Onde, para b0,b1∈B, os seguintes elementos são equivalentes:
(A,Sb0b1E)=(A,βsb1b0βe),∀βs,βe∈S∪{σ}
Outro ponto importante é que todo elemento na palavra na segunda posição da tupla precisa
ser distinto, e toda string string em B com pelo menos um elemento é aceita em S:
b∈B⟹b∈S∀β0b0β1b1β3∈S⟹b0,b1∈B,b0=b1,β0,β1,β2∈S∪{σ}
Um elemento a∈A qualquer só pode aparecer uma única vez no lado esquerdo
da tupla.
Nesse sentido, as duas transições acima mencionadas da Máquina de Turing arbitrária seriam representadas assim:
((q0,σ0),((q1,σ1,⇐),(q2,σ2,⇒)))
Ou, em outras palavras, A=Q×Γ;B=Q×Γ×{⇐,⇒}
Isso nos permite montar um conjunto de tuplas (A,B) que equivalam ao conjunto de tuplas
(A,B+); vamos chamar o mapemaento (A,B) de mapeamento de transições, enquanto que
o (A,B+) é o mapeamento completo.
Os dois modelos são equivalentes.
Demonstração, mapeamento completo para mapeamento de transição
Tome um elemento do mapeamento de transição t∈δ,t:(a,bβ), com a∈A, b∈B e β∈B∗.
Pela definição, ∀tx∈δ,tx[0]=a⟹tx=t. Isso significa que t é a única transição
que tem como argumentos a, produzindo um dos elementos dentro de bβ.
Mapeemos para transições simples. Vamos aplicar um algoritmo recursivo para gerar um conjunto de transições (A,B):
mapeamento_simples(a,bβ)↦{(a,b)}∪mapeamento_simples(a,β)mapeamento_simples(a,σ)↦∅
No exemplo do mapeamento da máquina de Turing acima:
mapeamento_simples((q0,σ0),((q1,σ1,⇐),(q2,σ2,⇒)))↦{((q0,σ0),(q1,σ1,⇐))}∪mapeamento_simples((q0,σ0),((q2,σ2,⇒)))↦{((q0,σ0),(q1,σ1,⇐)),((q0,σ0),(q1,σ1,⇒))}∪mapeamento_simples((q0,σ0),σ)↦{((q0,σ0),(q1,σ1,⇐)),((q0,σ0),(q1,σ1,⇒))}
Demonstração, mapeamento de transição para mapeamento completo
Aqui, temos um conjunto de pares (A,B) e gostaríamos de juntar tudo que tenha o mesmo LHS e gerar uma lista do RHS. Seria o equivalente
Java a:
List<Par<A, B>> transicoes = ...;
Map<A, List<B>> mapemaentoCompleto = transicoes.stream()
.collect(Collectors.groupingBy(Par::LHS,
Collectors.mapping(Par::RHS, Collectors.toList())));
Máquina de Turing
Uma máquina de Turing é uma séptupla ⟨Q,q0,F,Σ,b,Γ,δ⟩ onde:
- Q é o conjunto de todos os estados
- q0 é o estado inicial, q0∈Q
- F é o conjunto de estados de aceitação, F⊆Q
- Σ é o conjunto de elementos da entrada, Σ⊆Γ∖{b}
- b é o símbolo de espaço em branco, b∈Γ
- Γ é o conjunto de todos os elementos de trabalho, os símbolos da fita
- δ são as transições, sempre mapeamento de um estado e um símbolo na cabeça de leitura para outro
estado, o novo símbolo que ficará no lugar do símbolo lido e também se a cabeça de leitura seguiu para
a esquerda ou para a direita, (Q∖F,Γ)↦(Q,Γ,{⇐,⇒})
Ao alcançar um estado final qf∈F, como não tem transição para esse estado, alcança-se a aceitação.
Caso se esteja em um estado não final q∈Q,q∈F com um símbolo de fita γ e não seja
possível disparar alguma transição, então a entrada foi rejeitada.
Autômato de fila
Um autômato de fila é uma sextupla ⟨Q,q0,Σ,$,Γ,δ⟩ onde:
- Q é o conjunto de todos os estados
- q0 é o estado inicial, q0∈Q
- Σ é o conjunto de elementos da entrada, Σ⊆Γ∖{$}
- $ é o símbolo que representa o final da palavra, $∈Γ
- Γ é o conjunto de todos os elementos de trabalho
- δ são as transições, sempre mapeamento de um estado e um símbolo da fita para um novo estado
e, evantualmente, a inserção de uma string Γ∗ no final da fila.
Diz-se que houve aceitação ao, no final do processamento, a fila estar vazia. Caso a fila não esteja vazia e não
tenha mais transição para disparar, aconteceu a rejeição de uma palavra.
Simulando um autômato de fila em uma Máquina de Turing
Temos um autômato de fila ⟨Q,q0,Σ,$,Γ,δ⟩. Precisamos de uma Máquina de Turing que
se comporte exatamente como esse autômato de fila.
Vamos iniciar com a fita tendo apenas a palavra de entrada, sem o $, pois estamos numa Máquina de Turing, correto?
Aqui, o foco inicial será o autômato de fila que reconhece a palavra AnBnCn. Vamos explorar esse exemplo sem
perder generalidade:
Onde a seta para baixo mostra a cabeça de leitura da Máquina de Turing. O estado está indicado acima da cabeça de
leitura, no caso, qi. Símbolos em branco à esquerda ou à direita serão omitidos ou motrados conforme proveito. Por exemplo,
a máquina está na estado qj dois espaços em branco antes da entrada:
Bem, na simulação da autômato de fila, apenas mantemos a fila e o estado da máquina, sem maiores indicações. Isso permite,
por exemplo, colocar a evolução do autômato assim, com cada transição sendo uma linha:
q0: AAABBBCCC$
qa: AABBBCCC$
qa: ABBBCCC$A
qa: BBBCCC$AA
qb: BBCCC$AA
qb: BCCC$AAB
qb: CCC$AABB
qc: CC$AABB
qc: C$AABBC
qc: $AABBCC
q0: AABBCC$
Um autômato de fila para AnBnCn
Como motivador para a transformação, vamos iniciar com o autômato de fila e então aplicar regras de conversão
para Máquina de Turing. Então, como definir esse autômato? Vamos pelas informações conhecidas: começa em q0,
tem os símbolos de entrada Σ={A,B,C}, e tem o símbolo terminal $.
Um ponto importante é que ele precisa reconhecer a palavra gerada quando n=0, portanto ϵ, a palavra
vazia. Isso se dá usando a seguinte transformação:
(q0,$)↦(q0,ϵ)
Executando o autômato apenas com essa regra passando a palavra vazia para ele:
Como a única opção foi consumir o $ sem produzir nada. A fila ficou vazia após esse consumo, portanto
houve o aceite da entrada.
Agora, e para os outros casos? Meu pensamento aqui é simples:
- seja Θ0,Θ1∈[ABC]∗
- seja a fila AAxΘ0$Θ1
- esteja o autômato em um estado qx=qa
- então a transição (qx,A)↦(qa,ϵ) existe
- e a transição (qa,A)↦(qa,A) também existe
- portanto, após x+1 transições, sairemos de qx:AAxΘ0$Θ1 para qa:Θ0$Θ1Ax
Note que os estados qx,qa e as duas transições descritas acima vão consumir exatamente um único elemento
de uma sequência de As e jogar o resto da sequência para o final. Podemos fazer coisas equivalentes para
B e para C. Detalhe que, no caso de C, ao encontrar $, podemos usar a estratégia de jogar $ no final
e voltar para q0. Se chegou nesse ponto, então saímos de q0:AAxBBxCCx$ para q0:AxBxCx$. Afinal,
consumimos sempre um elemento de uma sequência de A, B ou C e jogamos o resto para o final da fila. Basicamente
reduzimos o problema com n=x+1 para n=x, até o ponto de encontrar n=0 que já sabemos reconhecer.
Por questões de simplicidade, usemos qy para B o que o qx é para o A, e equivalentemente qz para o C.
qb e qc são equivalentes ao qa no sentido que são produzidos pelo qx ou equivalente e jogam o resto da
sequência no final da fila.
No caso das transições usando A, temos que a primeira possibilidade para qx é q0, pois o sistema iniciará
exatamente em q0 e necessita consumir um A ou aceitar a palavra vazia. Não descartemos, ainda, outras possibilidades
para qx.
Similarmente, chegaremos na sequência de B através de qa, então uma possibilidade para qy seria justamente
qa. E para qc, temos que chegará da sequência de Bs, portanto qb é uma das possibilidades para qz.
Assim, temos as seguintes transições definidas:
(q0,$)(q0,A)(qa,A)(qa,B)(qb,B)(qb,C)(qC,C)(qC,$)↦↦↦↦↦↦↦↦(q0,ϵ)(qa,ϵ)(qa,A)(qb,ϵ)(qb,B)(qc,ϵ)(qc,C)(q0,$)
Ok, agora isso realmente reconhece o que desejamos? Vamos ver…
Se tivermos por acaso q0 tentando consumir B ou C, não tem transição. O autômato de fila não consegue
disparar nenhuma transição e não está vazio, portanto rejeitou a entrada. Logo, recusa entradas no formato
[BC][ABC]∗.
Saindo de qa, se for um C, trava também. Logo, entradas do tipo A+C[ABC]∗ também são recusadas. Se chegar
no final da palavra, também recusa, daí A+ também é rejeitado. De modo semelhante, também se recusa quando
em qb encontrar um A ou o final da palavra, ou quando em qc encontrar um A ou um B. Logo, as únicas
opções são um subconjunto de A+B+C+∣ϵ. Tomemos a forma genérica AxByCz, com x,y,z≥0. Note
que no caso x=y=z=0 temos ϵ, que é aceito.
Esse autômato é de tal forma que sempre repete os mesmos estados nessa ordem: q0↦qa↦qb↦qc↦q0. Já vimos que para ocorrer essa transição toda de q0 para q0 novamente consumimos necessariamente 1
A, 1 B e 1 C. Portanto, do estado inicial q0:Ax+1By+1Cz+1$ iremos naturalmente para q0:AxByCz$.
Chamemos essa operação de “rodar um ciclo”. Suponha agora que x,z>y. Isso significa que poderemos rodar no máximo
y ciclos. Após rodar y ciclos, teremos que o autômato de fila estará q0:Ax−yCz−y$. Porém A+C+ não é
reconhecido, pois é um subconjunto de A+C[ABC]∗ e já vimos que esse conjunto não é reconhecido. Logo, não podemos ter
x,z>y. Agora, e se x>y≥z? Isso ainda é possível… Então, após rodar z ciclos, teremos q0:Ax−zBy−z$.
Isso é uam palavra em A+B∗. O autômato recusa A+, portanto ainda tem A+B+, porém vimos já que ele não aceita
esse tipo de entrada, portanto também recusa palavras em A+B+. Portanto, chegamos a conclusão que x≤y.
Usando raciocínio semelhante iremos encontrar que x≤z. Assim, podemos fazer a hipótese de y=z.
Como x≤y e x≤z, temos que y−x≥0 e z−x≥0. Portanto, após rodar x ciclos, teremos
o autômato de fila assim: q0:By−xCz−x. Se y−x=0, teremos um subconjunto de B+C∗, porém
já vimos que entradas [BC][ABC]∗ são rejeitadas. Portanto, y−x=0. Isso nos leva a crer que z−x>0,
pois y=z. Com isso, teremos C+, que também é uma entrada rejeitada por também ser um subconjunto de
[BC][ABC]∗. Logo, temos que x≤y,z=y. Com um esforço semelhante, temos que se x<y não
iremos reconhecer a palavra, logo só nos resta x=y=z. Então, esse autômato de fila realmente
reconhece a linguagem desejada, e apenas ela.
Definindo o autômato de fila:
Q={q0,qa,qb,qc}q0 eˊ o estado inicialΣ={A,B,C}$ eˊ o indicador de final de palavraΓ={A,B,C,$}δ=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(q0,$)(q0,A)(qa,A)(qa,B)(qb,B)(qb,C)(qC,C)(qC,$)↦↦↦↦↦↦↦↦(q0,ϵ)(qa,ϵ)(qa,A)(qb,ϵ)(qb,B)(qc,ϵ)(qc,C)(q0,$)⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫
Simulando através de uma Máquina de Turing
Inicialmente, vamos pegar a entrada e transformá-la de modo digno. Na Máquina de Turing a entrada
será necessariamente apenas a palavra. Logo, para simular melhor o autômato de fila, nada como
transformar a entrada da Máquina de Turing na entrada do autômato de fila.
Portanto, para o estado inicial da Máquina de Turing qt, temos de sair de
para
onde q0′ é o equivalente ao q0 do autômato de fila.
Seja qt o estado inicial da Máquina de Turing, o objetivo dela é único e simplesmente inserir o símbolo
terminador $ no final da entrada. Logo, todo e qualquer símbolo da entrada deverá permanecer inalterado
enquanto a Máquina de Turing caminha para a direita até encontrar o primeiro branco, então substituirá esse
branco por $ e passará a caminhar à esquerda para voltar para o início.
Exemplificando, sairemos de
passaremos por alguns estágios intermediários como
até chegarmos em
Nesse momento, o espaço em branco será substituído por $ e o estado mudará para qi=qt, que é o estado
que iremos usar apenas para fazer o rebobinar. Então, o próximo passo é
iremos passar por alguns estados intermediários como
e finalmente iremos ultrapassar o início da entrada:
Nesse momento, iremos manter o branco ali e caminhar a direita, assumindo o estado q0′:
como gostaríamos.
Agora, vamos usar a operação de rebobinar em diversos momentos, pois iremos escrever coisas no final da fita
para representar o que é produzido no final do disparo do autômato de fila. Portanto, podemos deixar um marcador
especial que, ao rebobinador encontrar esse marcador, ele irá para um estado específico mapeado do autômato de
fila. Como no autômato de fila usamos q0, qa e assim por diante, usarei esse subscrito para representar
esse estado. Isso significa que o começo do nosso processamento não é mais ir para a direita e colocar um $ no
final da entrada, mas sim ir para a esquerda, inserir 0 na entrada, então ir para a direita para inserir o $
no final, então rebobinar tudo e iniciar o processamento do autômato de fila. Então, chamemos de qg o estado inicial
da Máuqina de Turing.
qg tem como única intenção ir para a esquerda mantendo o caracter inicial, escrever 0 no espaço em branco e ir
para a direita com o qt já definido.
A execução fica assim:
Todo o resto continua sendo bem equivalente, mas temos que qi irá consumir 0 e irá para a direita
no estado q0′:
Por algo que irei explicar mais tarde, vamos usar qt$ no lugar de qt, mas ele faz exatamente o que foi definido para
qt: vai para a direita e, ao achar um estado em branco, produz $ e entra no estado de rebobinar.
Só aqui, para determinar alguns elementos da Máquina de Turing, temos algumas definições:
- todo estado do autômato de fila implica em um símbolo de trabalho da Máquina de Turing e também um estado
da Máquina de Turing
- vamos chamar o mapeamento de estado do autômato de fila para elemento de trabalho da função τ:QAF↦ΓMT
- vamos chamar o mapeamento de estado do autômato de fila para estado da máquina de Turing da função χ:QAF↦QMT
- o alfabeto de entrada do autômato de fila é o mesmo alfabeto de entrada da Máquina de Turing, ΣAF≡ΣMT
- $ pertence ao alfabeto de trabalho da Máquina de Turing (ou algo equivalente a ele)
- não há equivalente ao branco no autômato de fila, portanto ∀γ∈ΓAF,t(γ)=b,
sendo t:ΓAF↦ΓMT a função que mapeia elementos de trabalho do autômato de fila para
elementos de trabalho da Máquina de Turing
- de modo similar, não há equivalente do branco dos estados do autômato de fila na fita de trabalho da Máquina
de Turing, ∀q∈QAF,τ(q)=b, onde τ:QAF↦ΓMT transforma o estado
do autômato de fila em um símbolo de trabalho da Máquina de Turing
- a Máquina de Turing começa no estado qg que tem as transições ∀σ∈Σ,(qg,σ)↦(qg,σ,⇐) e também (qg,b)↦(qt$,τ(q0),⇒), sendo q0 o estado
inicial do autômato de fila e qt$=qg.
- existem estados da máquina de Turing que não devem possuir equivalência no autômato de fila, vamos chamar
o conjunto desses estados de R, portanto ∀q∈QAF,χ(q)∈R, sendo χ:QAF↦QMT
a função que mapeia de um estado do autômato de fila para um estado na máquina de Turing
- qg,qt$,qi∈R
- para colocar o $ no final, temos que ter as seguintes transições ∀σ∈Σ,(qt$,σ)↦(qt$,σ,⇒) e também a transição definitiva de inserção do $, (qt$,b)↦(qi,$,⇐), sendo que qt$=qi (por outras questões temos também que qg=qi)
- para o rebobinar, temos que conseguir recuar sempre, não só para os símbolos da entrada como também para os símbolos
de trabalho do autômato de fila, portanto as transições ∀γ∈ΓAF,(qi,t(γ))↦(qi,t(γ),⇐) existem
- finalmente, temos que, após rebobinar, ir para o estado equivalente do autômato de fila, portanto as seguintes transições
existem ∀q∈QAF,(qi,τ(q))↦(χ(q),b,⇒)
Isso apenas para dar o bootstraping do autômato de fila. Agora precisamos definir as transições.
Vamos dividir essas transições em dois tipos: o tipo δϵ são transições que não produzem nada para o final
da fila (portanto, se a i-ésima transição for ti:(qx,γ)↦(qy,ϵ), então ti∈δϵ);
e o tipo δΩ, que produz um ou mais elementos no final da fila (portanto, se a i-ésimo transição for ti:(qx,γ)↦(qy,ω),ω∈Γ+, então ti∈δΩ).
As transições δϵ, como não produzem nada de especial no final, podem ser representadas na máquina de Turing
como simplesmente transformando o elemento atual em branco, mudando para o estado χ(qy) e avançando para a direita:
∀ti=(qx,γ)↦(qy,σ)∈δϵ,(χ(qx),t(γ))↦(χ(qy),b,⇒)
Para transições δΩ, vamos deixar a marca do novo estado do autômato de fila para quando for feita a rebobinação.
Nessa situação, precisamos ir até o final e inserir exatamente o elemento produzido. Peguemos a transição tj∈δΩ,tj=(qx,γ)↦(qy,γω),γ∈ΓAF,ω∈ΓAF∗. Para essa transição, precisamos
de um novo qtγω∈R que faça um papel semelhante ao qt$ previamente definido: ir até o final da entrada
e, então, inserir o equivalente à palavra γω no final da fita, então mudar para o estado de rebobinar qi.
Nomeemos então o conjunto de estados QΩ, onde qtω inQΩ se ω∈ΓAF+. Note que ∀qtω∈QΩ,qtω∈R,qtω=qi,qtω=qg. Uma das característica dos estados em
QΩ é que, para elementos de fila mapeados vindos de f(γ),γ∈ΓAF, ele simplesmente irá ignorar esse
elemento e seguir para a direita, até encontrar o primeiro elemento em branco que, então, começará a fazer o dump do ω na
fita:
∀qtω∈QΩ,∀γ∈ΓAF,(qtω,t(γ))↦(qtω,t(γ),⇒)
Note que a premissa original gera u subconjunto dessas transições, já que ΣAF⊆ΓAF∖{$}.
Quando chega no elemento em branco, temos duas opções para qtω: ∣ω∣=1 ou então ∣ω∣>1. Para o primeiro
caso, tomemos qtγ,γ∈ΓAF; vamos chamar esse conjunto de QΩ1. Ele vai simplesmente colocar na
fita o t(γ) e seguir rebobinando, portanto:
∀qtγ∈QΩ1,γ∈ΓAF,(qtγ,b)↦(qi,t(γ),⇐)
Note que, quando γ=$, o caso para qt$ é apenas um caso especial disso.
Para os outros elementos, adotemos a nomenclatura qtγω,γ∈ΓAF,ω∈ΓAF+;
vamos chamar esse conjunto de QΩ2+. Ele vai colocar na fita o elemento t(γ) e irá para a direita para
terminar de colocar o resto do mapeamento de ω. Podemos assumir então que ele irá para o estado qtω tal
que qtω∈QΩ:
∀qtγω∈QΩ2+,γ∈ΓAF,(qtγω,b)↦(qtω,t(γ),⇒),qtω∈QΩ
Vale ressaltar que QΩ=QΩ1+QΩ2+,QΩ1∩QΩ2+=∅.
Essa regra, definida exatamente desse jeito, garante que o elemento produzido pela transição do autômato seja fielmente colocada
apenas no final da fila.
Recapitulando:
- todo estado do autômato de fila implica em um símbolo de trabalho da Máquina de Turing e também um estado
da Máquina de Turing
- vamos chamar o mapeamento de estado do autômato de fila para elemento de trabalho da função bijetiva τ:QAF↦ΓQ,
sendo ΓQ⊂ΓMT
- vamos chamar o mapeamento de estado do autômato de fila para estado da máquina de Turing da função bijetiva χ:QAF↦QQ,
sendo QQ⊂QMT
- QMT=R+QQ
- QQ∩R=∅
- os alfabetos de entrada são equivalentes, ΣAF≡ΣMT
- o indicador de fim de linha $ no autômato de fila tem seu equivalente na máquina de Turing, representado simplesmente
por $
- todo elemento de trabalho do autômato de fila tem um equivalente no elemento de fita, ∀γ∈ΓAF,t(γ)∈ΓΓ, sendo ΓΓ⊂ΓMT
- ΓΓ∩ΓQ=∅
- seja b o caracter que representa o vazio da fita da máquina de Turing, b∈ΓΓ+ΓQ
- QΩ⊂R,QΩ=QΩ1+QΩ2+,QΩ1∩QΩ2+=∅
- ∀γ∈ΓAF,∃qγ∈QΩ1
- qg,qi∈R
- qg,qi∈QΩ
- estado inicial da máquina de Turing é qg∈R, cujas únicas transições são ∀σ∈Σ,(qg,σ)↦(qg,σ,⇐) e também (qg,b)↦(qt$,τ(q0),⇒),qt$∈QΩ1
- as seguintes transições existem, ∀qtω∈QΩ,∀γ∈ΓAF,(qtω,t(γ))↦(qtω,t(γ),⇒)
- seja uma transição do autômato de fila que produza a string não vazia ω∈ΓAF+, então temos um estado
qtω∈QΩ; se ∣ω∣≥2, então qtω∈QΩ2+, caso contrário ∣ω∣=1,
então qtω∈QΩ1
- seja qtγω∈QΩ2+,γ∈ΓAF,ω∈ΓAF+, então temos que
qtω∈QΩ; se ∣ω∣≥2, então qtω∈QΩ2+, caso contrário ∣ω∣=1,
então qtω∈QΩ1
- existem as transições ∀qtω∈QΩ,∀γ∈ΓAF,(qtω,t(γ))↦(qtω,t(γ),⇒)
- existem as transições ∀qtγ∈QΩ1,(qtγ,b)↦(qi,t(γ),⇐)
- existem as transições ∀qtγω∈QΩ2+,(qtγω,b)↦(qtω,t(γ),⇒)
- seja o estado de rebobinar qi∈R, então ele tem apenas as seguintes transições:
- ∀γ∈ΓAF,(qi,t(γ))↦(qi,t(γ),⇐)
- ∀q∈QAF,(qi,τ(q))↦(χ(q),b,⇒)
- se a transição do autômato de fila for t∈δϵ,t:(qx,γ)↦(qy,ϵ),qx,qy∈QAF,γ∈ΓAF,
então a seguinte transição existe (χ(qx),t(γ))↦(χ(qy),b,⇒)
- se a transição do autômato de fila for t∈δΩ,t:(qx,γ)↦(qy,ω),qx,qy∈QAF,γ∈ΓAF,ω∈ΓAF+, então a seguinte transição existe (χ(qx),t(γ))↦(qtω,τ(qy),⇒),qtω∈QΩ
- para simular a aceitação, que acontece se e somente se o autômato de fila consumir todos os elementos da entrada, temos que todo
estado composto por equivalência do autômato de fila quando consumir o branco deve ir para o estado de aceitação qf∈F⊂R, tal que
qf∈QΩ+{qg,qi}
- portanto, as seguintes transições existem ∀q∈QAF,(χ(q),b)↦(qf,b,⇒)
Em cima dessas, regras, para o autômato de fila que reconhece AnBnCn:
QAF={q0,qa,qb,qc}q0 eˊ o estado inicialΣAF={A,B,C}$ eˊ o indicador de final de palavraΓAF={A,B,C,$}δ=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧(q0,$)(q0,A)(qa,A)(qa,B)(qb,B)(qb,C)(qC,C)(qC,$)↦↦↦↦↦↦↦↦(q0,ϵ)(qa,ϵ)(qa,A)(qb,ϵ)(qb,B)(qc,ϵ)(qc,C)(q0,$)⎭⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎫
Temos que as seguintes transições são do tipo δΩ:
(qa,A)(qb,B)(qC,C)(qC,$)↦↦↦↦(qa,A)(qb,B)(qc,C)(q0,$)
e as seguintes são do tipo δϵ:
(q0,$)(q0,A)(qa,B)(qb,C)↦↦↦↦(q0,ϵ)(qa,ϵ)(qb,ϵ)(qc,ϵ)
Todas as transições δΩ geram exatamente um único caracter na saída, portanto temos
que QΩ2+=∅, portanto:
QΩ=QΩ1QΩ1={qt$,qtA,qtB,qtC}
Também temos que:
ΓΓ={$,A,B,C}ΓQ={τ(q0),τ(qa),τ(qb),τ(qc)}QQ={χ(q0),χ(qa),χ(qb),χ(qc)}
Portanto, temos o seguinte a cerca dos estados e símbolos da máquina de Turing:
Q={qg,qf,qi,qt$,qtA,qtB,qtC,χ(q0),χ(qa),χ(qb),χ(qc)}qg eˊ o estado inicialF={qf}ΣMT={A,B,C}b eˊ o sıˊmbolo vazio da fitaΓMT={$,A,B,C,τ(q0),τ(qa),τ(qb),τ(qc),b}
Faltando definir, portanto, apenas as transições. Temos as seguintes fornecidas pelo estado de rebobinar, estado inicial e
avanços dos estados qω∈QΩ antes de inserir na fita os estados:
(qg,A)(qg,B)(qg,C)(qg,b)(qi,$)(qi,A)(qi,B)(qi,C)(qt$,A)(qtA,A)(qtB,A)(qtC,A)(qt$,B)(qtA,B)(qtB,B)(qtC,B)(qt$,C)(qtA,C)(qtB,C)(qtC,C)(qt$,$)(qtA,$)(qtB,$)(qtC,$)↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦↦(qg,A,⇐)(qg,B,⇐)(qg,C,⇐)(qt$,τ(q0),⇒)(qi,$,⇐)(qi,A,⇐)(qi,B,⇐)(qi,C,⇐)(qt$,A,⇒)(qtA,A,⇒)(qtB,A,⇒)(qtC,A,⇒)(qt$,B,⇒)(qtA,B,⇒)(qtB,B,⇒)(qtC,B,⇒)(qt$,C,⇒)(qtA,C,⇒)(qtB,C,⇒)(qtC,C,⇒)(qt$,$,⇒)(qtA,$,⇒)(qtB,$,⇒)(qtC,$,⇒)
Das transições dos estados qω∈QΩ colocando os símbolos no final da fila:
(qt$,b)(qtA,b)(qtB,b)(qtC,b)↦↦↦↦(qi,$,⇐)(qi,A,⇐)(qi,B,⇐)(qi,C,⇐)
Das transições vindos do final do rebobinar, recuperando o estado em ΓQ:
(qi,τ(q0))(qi,τ(qa))(qi,τ(qb))(qi,τ(qc))↦↦↦↦(χ(q0),b,⇒)(χ(qa),b,⇒)(χ(qb),b,⇒)(χ(qc),b,⇒)
Das transições disponíveis no autômato de fila:
(χ(q0),$)(χ(q0),A)(χ(qa),B)(χ(qb),C)(χ(qa),A)(χ(qb),B)(χ(qc),C)(χ(qc),$)↦↦↦↦↦↦↦↦(χ(q0),b,⇒)(χ(qa),b,⇒)(χ(qb),b,⇒)(χ(qc),b,⇒)(qtA,τ(qa),⇒)(qtB,τ(qb),⇒)(qtC,τ(qc),⇒)(qt$,τ(q0),⇒)
Das transições terminadoras, que levam a qf:
(χ(q0),b)(χ(qa),b)(χ(qb),b)(χ(qc),b)↦↦↦↦(qf,b,⇒)(qf,b,⇒)(qf,b,⇒)(qf,b,⇒)
Assim, conseguimos escrever uma Máquina de Turing que consegue simular o comportamento de um autômato de fila.
Eis a execução para o reconhecimento de AAABBBCCC:
aqui, estou usando 0 para representar τ(q0), a para representar τ(qa), b para representar τ(qb),
c para representar τ(qc) na fita. Estados do tipo χ(qx) são representados simplesmente como qx.
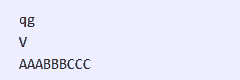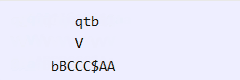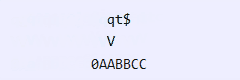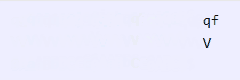
Com isso, terminamos a primeira parte desta demonstração. O próximo passo é provar que podemos usar autômatos de fila para rodar
máquinas de Turing, não importa o quão complicadas elas sejam.