Baseado na minha resposta sobre a pergunta O que é assíntota?

Um conto grego

A assíntota de Aquiles é a tartaruga

Corolário do Paradoxo de Zeno

Um dia, Aquiles, o Herói, e uma tartaruga discutiram. A tartaruga afirmou para Aquiles que, se ela começasse na frente, ela iria vencer uma corrida de qualquer distância contra o Herói. Curioso, Aquiles perguntou

-Por que disso? Se eu sou mais rápido que você, eu irei vencer.

Para então a tartaruga responder:

-Se eu começar na frente, você precisa primeiro alcançar a posição que eu estava. Mas até você chegar lá, eu terei andado, estarei mais adiante. Então, você deverá chegar a minha nova posição, e eu estarei na sua frente. Então você precisará de infinitos passos desses até chegar em mim, pois então para me ultrapassar precisará de mais do que infinitos passos.

Noção informal de assíntota

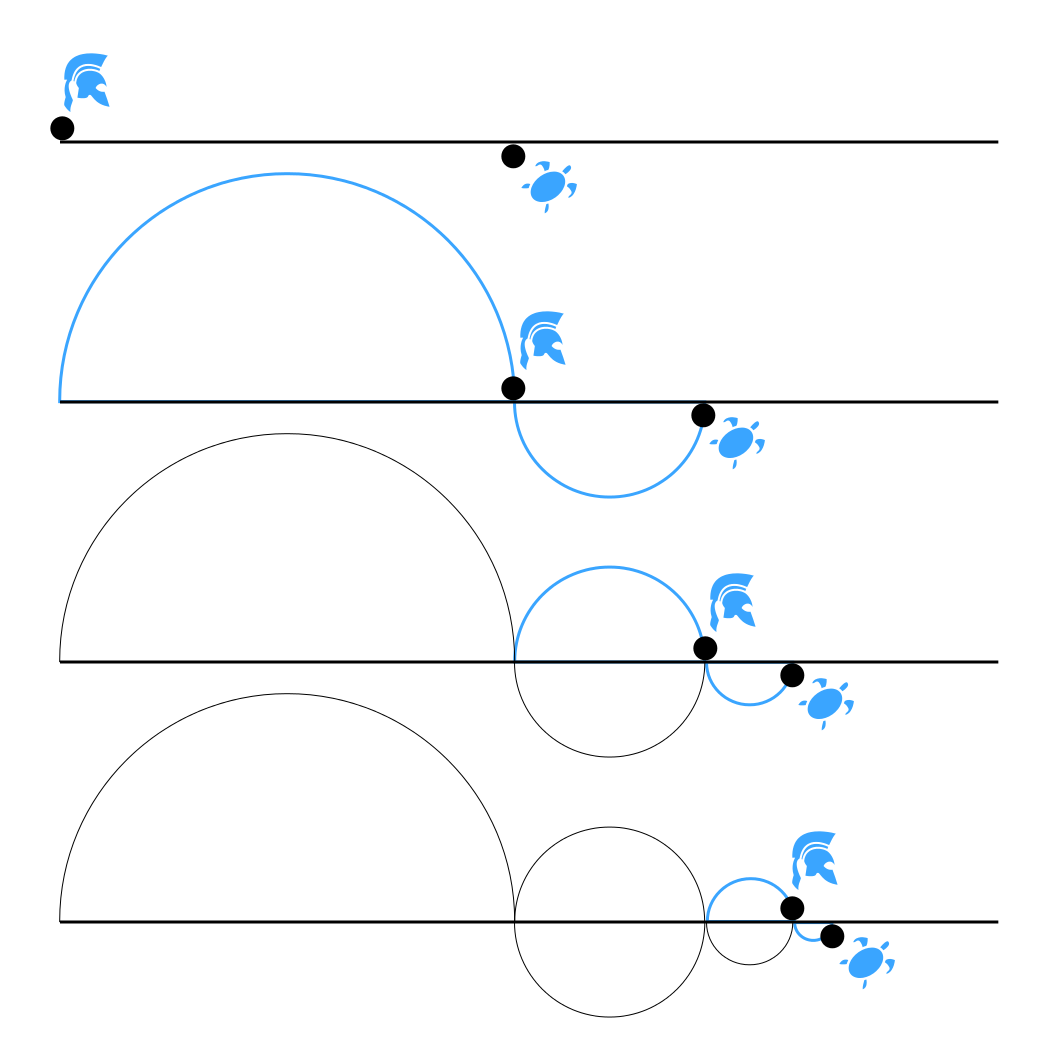
No paradoxo de Zeno, não importa quantas vezes Aquiles tente ultrapassar a tartaruga, ele nunca conseguirá. Pois, a cada passo, Aquiles está se aproximando da tartaruga. Aquiles se torna assintoticamente próximo da tartaruga.

Veja os seguinte infográfico, evolução das posições de Aquiles e da tartaruga:

Dá para perceber que Aquiles fica cada vez mais próximo da tartaruga a cada passagem de tempo. A esse tipo de comportamento nós chamamos de assíntota. Daí, a assíntota de Aquiles é a tartaruga.

Quando você quer saber o comportamento geral de uma função, você quer saber qual a assíntota da função. Por exemplo:

$f(x) = \frac{x^2 - x}{2}$

Ao infinito, essa função tende a ter o mesmo comportamento que $x^2$ . Então podemos dizer que o comportamento de $f(x) = \frac{x^2 - x}{2}$ é assintoticamente $x^2$ .

Isso tem aplicação prática?

Bem, isso quer dizer que o bubble sort piora tão rápido quando o insertion sort, e também que o merge sort será melhor em casos maiores. Mais tarde, na seção Por que isso importa para o programador?, eu detalharei mais.

Como identificar assíntotas?

De modo geral, você precisa de um “Aquiles” e de uma “tartaruga”. A tartaruga será a assíntota de Aquiles.

A função dada como exemplo ela se aproxima de $x^2$ , mas nunca chega nela.

Outro caso também, eu poderia pegar a função $\frac{1}{x}$ . No infinito positivo, ela tende a ser zero, mas nunca o é:

Note que quando $x=10$ , a função vale 0.1. Quando $x=80$ , a função por sua vez agora valeria 0.0125. Ficando cada vez mais próxima de 0, mas nunca de fato chegando lá.

Por que isso importa para o programador?

Em um mundo normal de aplicações corporativas que não se preocupam em calcular qual o desconto (em porcentual) que eu devo aplicar no preço de venda para que o valor com o ICMS-ST alcance o total de R$10,00 no preço final (dica: tem uma fórmula que condensa a soma infinita), assíntotas servem basicamente para descrever comportamentos de algoritmos.

Então, para o programador médio, o que importa é comportamento assintótico, normalmente associado à complexidade temporal/espacial de um algoritmo.

A seguir, uma lista de perguntas que flertam com esse conceito (o autor sabendo disso ou não):

Como provar a ordem assintótica de um algoritmo?
Existe algum algoritmo de ordenação que execute realmente em O(n)?
Consumo de tempo em código cúbico
Como melhorar o desempenho de meu código com “for”?
Nota especial: nessa pergunta, o autor acreditava que ter 3 for aninhados um dentro do outro era sinal de ineficiência, mas ele não havia percebido que estava no melhor possível matematicamente para iterar em uma coleção “cúbica” de dados
Complexidade temporal de algoritmo palíndromo recursivo
Qual a melhor implementação do ‘Algoritmo MergeSort’?

Em todos os casos, se pede algo em relação ao comportamento assintótico (ou como parte da resposta, ou como parte da pergunta).

Também vale para o programador saber que comportamento assintótico nem sempre é tudo. As vezes temos constantes escondidas que, quando não se está “perseguindo tartarugas no infinito”, se tornam muito mais importantes. Por exemplo, o quick sort possui o tempo de execução normalmente mais rápido do que o merge sort.

Como provar a ordem assintótica de um algoritmo?

Esta pergunta já tem uma resposta aqui:

Como provar a ordem assintótica de um algoritmo? 3 respostas

Formalmente, o que é uma assíntota?

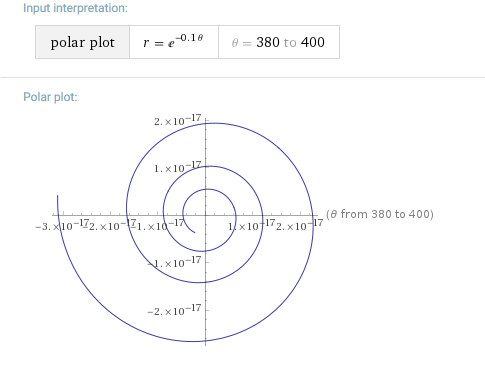
Uma assíntota é um ponto ou curva para o qual uma função tende. Por exemplo, o centro é a assíntota para a seguinte função polar exponencial:

$f(\theta) = e^{-0.1\times \theta}$

Ela é plotada assim:

Quanto maior o $\theta$ , mais próxima a função fica de $(0,0)$ . Então $(0,0)$ é a assíntota de $f(\theta) = e^{(-0.1\times \theta)}$ .

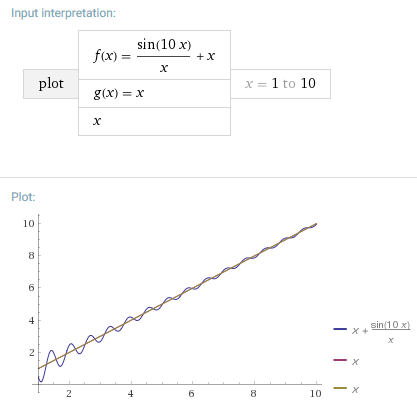
Uma curva pode interceptar sua assíntota. Por exemplo, $f(x) = \frac{\sin(10\times x)}{x} + x$ tem como assíntota $g(x) = x$ :

Nem toda assíntota precisa ser uma reta, mas pode ser uma curva. Como o caso de $f(x) = \left|\frac{1}{x}\right| + x^2$ , cuja assíntota nos infinitos é $g(x) = x^2$ :

Então, a assíntota $A$ de uma função $F$ é um valor (exemplo da espiral) ou função (outros dois exemplos) que, dada a evolução de $F$ em termo de alguma variável, $F$ se aproxima arbitrariamente próxima de $A$ .

Como descobrir uma assíntota de uma função?

Eu normalmente uso os seguintes passos (para funções que usam coordenadas cartesianas, não polares) para descobrir a ordem da assíntota:

conjecture $OA$
divida^* $\frac{F}{OA}$ ou $\frac{OA}{F}$
se errou, repita

A divisão, entretanto, não pode ser feita de qualquer forma. Normalmente, se deseja saber qual o comportamento extremo da função, então a divisão é com o limite da variável indo ao infinito. Nesse caso de comportamento no infinito, $OA$ é da mesma ordem da assíntota de $F$ se elas forem co-dominantes conforme definida nesta resposta:

$domina(f, g) = \begin{cases} dominada & \lim_{x\rightarrow \infty} \frac{f(x)}{g(x)} = 0\\ dominante & \lim_{x\rightarrow \infty} \frac{f(x)}{g(x)} = \infty\\ co-dominante & \lim_{x\rightarrow \infty} \frac{f(x)}{g(x)} = h(x), \exists x|h(x) \ne 0, \exists x|h(x) \ne \infty\\ \end{cases}$

Também condensado nessa resposta do @Isac para a mesma pergunta (obs: com $c \ne 0$ ):

$\lim_{n\rightarrow \infty} \frac{f(n)}{g(n)} = c$

Descoberta a ordem, o valor obtido pela divisão é o coeficiente do maior termo. Isso significa que o termo mais significante da assíntota tem coeficiente conhecido, $c$ . Agora, remova o termo mais significativa e calcule novamente. Como?

Bem, achamos $OA$ a função co-dominante de $F$ . Sabemos que $F = OA \times c + G$ , para $c = \lim \frac{OA}{F}$ . Então, agora, é achar o valor da assíntota de $G$ e somar a $c\times OA$ , fazendo isso recursivamente até que, em algum momento, $\lim G = 0$ . Essa será a curva da assíntota de $F$ .

Exemplo

Para $f(x) = x + \frac{\sin(10x)}{x}$ . Vamos primeiro supor que a ordem da função assintótica $OA$ é $x^2$ :

$\lim_{x\rightarrow\infty}\frac{x + \frac{\sin(10x)}{x}}{x^2} = \lim_{x\rightarrow\infty}\frac{x}{x^2} + \frac{\sin(10x)}{x^3}$

Essa divisão dá 0, portanto $OA$ domina $f(x)$ . Portanto, a primeira conjectura da ordem da função assintótica deu errado. Nesse caso, repitamos.

Vamos agora supor que a ordem da função assintótica $OA$ é $x$ :

$\lim_{x\rightarrow\infty}\frac{x + \frac{\sin(10x)}{x}}{x} = \lim_{x\rightarrow\infty}\frac{x}{x} + \frac{\sin(10x)}{x^2} \therefore \\ \lim_{x\rightarrow\infty}\frac{x + \frac{\sin(10x)}{x}}{x} = \lim_{x\rightarrow\infty}1 + 0 = 1$

Eles são co-dominantes, então a ordem assintótica é, realmente, $OA$ . Para o próximo passo, precisamos remover $c\times OA$ de $f(x)$ e verificar $g(x)$ :

$x + \frac{\sin(10x)}{x} - 1\times(x) = \frac{\sin(10x)}{x}$

Chegamos a conclusão que $g(x) = \frac{\sin(10 x)}{x}$ . Agora, precisamos de outro termo para definir a assíntota de $g(x)$ ?

$\lim_{x\rightarrow\infty}\frac{\sin(10x)}{x} = 0$

Não, não precisamos. Portanto, $A(x) = x$ é a assíntota para $f(x) = x + \frac{\sin(10\times x)}{x}$ .

Existem outras assíntotas que não as do infinito?

Sim, existem. Normalmente, elas se encontram em pontos de descontinuidade.

Tome a hipérbole $f(x) = \frac{1}{x}$ :

Ela apresenta descontinuidade em $x = 0$ . Portanto, o ponto $x = 0$ é um candidato a ser uma assíntota vertical da função. Para achar uma assíntota vertical no ponto $x = a$ , é preciso atender um desses quatro critérios:

$\lim_{x\rightarrow a^-}f(x) = \pm \infty\\ \lim_{x\rightarrow a^+}f(x) = \pm \infty$

A função deve tender ao infinito (positivo ou negativo) quando $x$ tender ao valor $a$ , seja o limite pela esquerda ou o limite pela direita.

No caso da hipérbole, quando $x \rightarrow 0$ pela direita, $f(x) \rightarrow +\infty$ . Isso já é o suficiente para considerar $x = 0$ hipérbole vertical de $\frac{1}{x}$ .

Fontes das imagens:

Testudo marginata (GPL): https://en.wikipedia.org/wiki/File:Nacht_006.jpg
O gif lide com isso, Aquiles portanto também deve ser usada sob a GPL
1 sobre x: https://en.wikipedia.org/wiki/File:Hyperbola_one_over_x.svg
Aquiles e a tartaruga: https://en.wikipedia.org/wiki/File:Zeno_Achilles_Paradox.png
Plotagem das funções obtidas de consultas ao WolframAlph: